Heron's formula
You can use Heron's formula to calculate the area of any triangle when you know the lengths of the three sides.
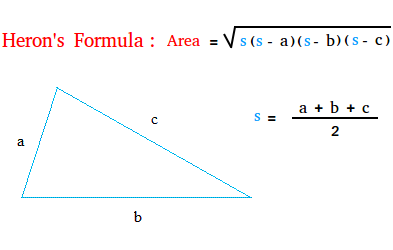
Heron's formula
Let us call the lengths of the three sides a, b, and c.
Let s be called the semi-perimeter.
The name makes sense because it is the perimeter divided by two.
Then, the formula to use to find the perimeter is the following.
Notice that you must first compute s or the semi-perimeter
A few examples showing how to use Heron's formula to calculate the area of triangles
Example #1:
Use Heron's formula to find the area of a triangle when a = 3 cm, b = 5 cm, and c = 4 cm
s = (3 + 5 + 4)/2 = 12/2 = 6
s − a = 6 − 3 = 3
s − b = 6 − 5 = 1
s − c = 6 − 4 = 2
s × (s − a) × (s − b) × (s − c) = 6 × 3 × 1 × 2 = 36
√(36) = 6
The area of this triangle is 6 cm2
Example #2:
Use Heron's formula to find the area of a triangle when a = 4 cm, b = 6 cm, and c = 8 cm
s = (4 + 6 + 8)/2 = 18/2 = 9
s − a = 9 − 4 = 5
s − b = 9 − 6 = 3
s − c = 9 − 8 = 1
s × (s − a) × (s − b) × (s − c) = 9 × 5 × 3 × 1 = 135
√(135) = 11.61
The area of this triangle is 11.61 cm2
Example #3:
Use Heron's formula to find the area of a triangle when a = 3/2 cm, b = 5/2 cm, and c = 2 cm
s = (3/2 + 5/2 + 2)/2 = (3/2 + 5/2 + 4/2)/2 = (12/2)/2 = 6/2 = 3
s − a = 3 − 3/2 = (6/2 − 3/2) = (6 − 3)/2 = 3/2
s − b = 3 − 5/2 = (6/2 − 5/2) = (6 − 5)/2 = 1/2
s − c = 3 − 2 = 1
s × (s − a) × (s − b) × (s − c) = 3 × 3/2 × 1/2 × 1 = 9/4
√(9/4) = 3/2
The area of this triangle is 1.5 cm2

