Adding fractions with the same or different denominators!

When adding fractions there are four important things you need to know and it is very important to keep these in mind to avoid common pitfalls. You could take the interactive fraction quiz to see how much you know! 

Fractions Quiz

Quiz completed 0 times

  • You cannot add the denominators, also called bottom numbers!
  • You can only add the numerators, also called top numbers!
  • You can add the numerators only when the denominators are the same!
  • If the denominators are not the same, look for a common denominator before adding the numerators.

Why can't you add the denominators when adding fractions?  

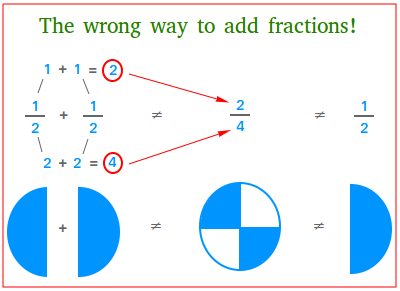
Let's illustrate why it does not make sense to add the denominators using an easy example. The figure below shows the wrong way to add 1 / 2 and 1 / 2. This mistake is quite common when learning fractions for the first time!

The wrong way to add fractions!

According to the figure above, if you could add the denominators, it would mean that adding half and half will still give half. Does this make sense? Of course not! 

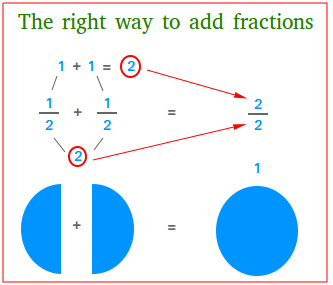
We all know that half a pizza plus another half of the same pizza is equal to 1 pizza as the following figure shows.

The right way to add fractions!

What have we learned so far?

  • You can only add the numerators when the denominators are the same for both fractions.
  • Since we don't add the denominators, the denominator stays the same.

Therefore, 1/2 + 1/2 = 1

Example #1

Add: 3/2 and 1/2

Observe that both fractions have the same denominator, which is 2. This means you can add the numerators (3 + 1 = 4) and your denominator will stay the same.

3 2 + 1 2 = (3 + 1) 2


3 2 + 1 2 = 4 2


3 2 + 1 2 = 2

What do we do then when adding fractions with different denominators?

When the denominators are different. you need to find equivalent fractions that give a common denominator for both fractions. All you need to do is the look for the least common multiple (LCM) of the denominators. 

Example #2:

2 3 + 3 6

Did you make the following observations for example #2 below?

  • The denominator is not the same for both fractions, so we cannot add 2 and 3 to get 5.
  • You need to look for a common denominator and then you can add the numerators.

Since 6 is the least common multiple of 3 and 6, you can use 6 as a common denominator.

Multiply the numerator and the denominator of 2 / 3 by 2, you will get 4 / 6

2 3 + 3 6 = (2×2) (3×2) + 3 6


2 3 + 3 6 = 4 6 + 3 6


2 3 + 3 6 = (4+3) 6


2 3 + 3 6 = 7 6

Example #3:

3 5 + 2 4

Notice that it is not easy to multiply one denominator by a number to get the second denominator as we did before in example #2.

As a rule of thumb, when the denominators do not have any common factor(s), you can just multiply them to get a common denominator. Since 4 and 5 have no common factors, the common denominator is 4 times 5 = 20.

3 5 + 2 4 = (3×4) (5×4) + (2×5) (4×5)


3 5 + 2 4 = 12 20 + 10 20


3 5 + 2 4 = (12+10) 20


3 5 + 2 4 = 22 20

Adding fractions with whole numbers

Here are the steps to follow when adding a fraction to a whole number.

Step 1

Convert the whole number into a fraction. You do this by using 1 as a denominator for the whole number.

Step 2

Look for the lowest common denominator. You just need to multiply 1 and the other denominator to get the lowest common denominator.

Step 3

Multiply the numerator and the denominator of the fraction in step 1 by the lowest common denominator. 

Step 4

Add the fractions.

Example #4

Add: 3/5 + 8

3/5 + 8 = 3/5 + 8/1 = 3/5 + 40/5 = (3 + 40)/5 = 43/5

If you understand the lesson about types of fractions and the lesson about comparing fractions, this lesson will be easy to follow. Check also fractions worksheets, where you can find a variety of worksheets about addition, subtraction, multiplication, and division of fractions in PDF format.

Adding fractions

Adding mixed numbers