Using the unit circle to find cosine and sine of 30 degrees and 60 degrees

Since we are using the unit circle, we need to put the 30-60-90 triangle inside the unit circle.

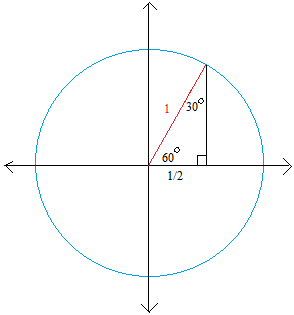
The radius of the circle is also the hypotenuse of the right triangle and it is equal to 1.

We have already seen in the previous lesson that the leg opposite the 30 degrees angle is half the hypotenuse. 

Again, we will find the length of vertical black line of the triangle using the pythagorean theorem.

Since 1/2 = 0.5, we will replace 1/2 with 0.5 in the formula to simplify the computation.

1² = 0.5² + y²

1 = 0.25 + y²

1 - 0.25 = 0.25 - 0.25 + y²

0.75 = y²

Since 0.75 = 3/4,   y = √ (3/4)

y = √(3) / √(4)

y = √(3) / 2

x = 1/2, y = √3 / 2 and t could be 30 or 60 degrees.

cos(30 degrees) = y / 1 = y = √3 / 2

cos(60 degrees) = x / 1 = x = 1 / 2

sin(60 degrees) = y / 1 = y = √3 / 2

sin(30 degrees) = x / 1 = x = 1 / 2