basic mathematics image
basic mathematics image

Proof of the area of a trapezoid


A first good way to start off with the proof of the area of a trapezoid is to draw a trapezoid and turn the trapezoid into a rectangle.


Trapezoid-image

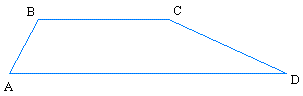
Look at the trapezoid ABCD above. How would you turn this into a rectangle?

Draw the average base (shown in red) which connects the midpoint of the two sides that are not parallel

Trapezoid-image

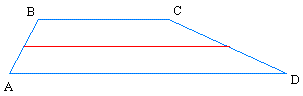
Then, make 4 triangles as shown below:

Trapezoid-image

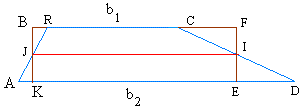
Let's call the two parallel sides in blue (the bases) b1 and b2

Since triangles EDI and CFI are congruent or equal and triangles KAJ and RBJ are equal, you could make a rectangle by rotating triangles EDI around point I, 180 degrees counterclockwise.

And by rotating triangle KAJ clockwise, but still 180 degrees around point J.

Because you could make a rectangle with the trapezoid, both figures have the same area

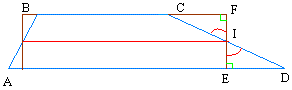
The reason that triangle EDI is equal to triangle IFC is because we can find two angles inside the triangles that are the same. If two angles are the same, then the third or last angle must be the same

The angles that are the same are shown below. They are in red and green. The angles in green are right angles. The angles in red are vertical angles

Trapezoid-image

This is important because if these two triangles are not congruent or the same, we cannot make the rectangle with the trapezoid by rotating triangle EDI. It would not fit properly

Again, this same argument applies for the two triangles on the left

Therefore, if we can find the area of the rectangle, the trapezoid will have the same area

Let us find the area of the rectangle.We will need the following figure again:

Trapezoid-image

First, make these important observations:

b1 = RC

BF = BR + b1 + CF

b2 = AD

KE = AD − AK − ED, so KE = b2 − AK − ED

AK = BR and ED = CF

Notice also that you can find the length of the line in red ( the average base ) by taking the average of length BF and length KE

Trapezoid-image

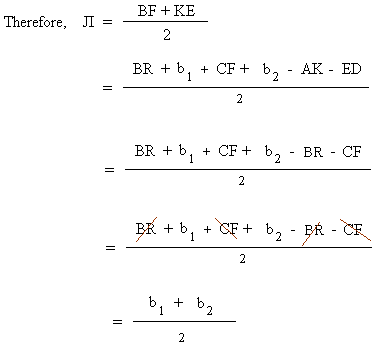Since the length of the line in red is the same as the base of the rectangle, we can just times that by the hegiht to get the area of the trapezoid


Finally, we get :

Trapezoid-image


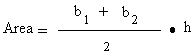An alternative proof of the area of a trapezoid could be done this way.

Start with the same trapezoid. Draw heights from From vertex B and C. This will break the trapezoid down into 3 shapes: 2 triangles and a rectangle.

Label the base of the small triangle x and the base of the bigger triangle y

Label the small base of the trapezoid b1 and b2

Trapezoid-image

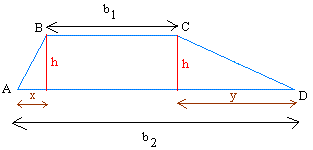b1 = b2 − ( x + y), so x + y = b2 − b1

The area of the rectangle is b1 × h, but the area of the triangles with base x and y are :



Trapezoid-image

To get the total area, just add these areas together:

Trapezoid-image

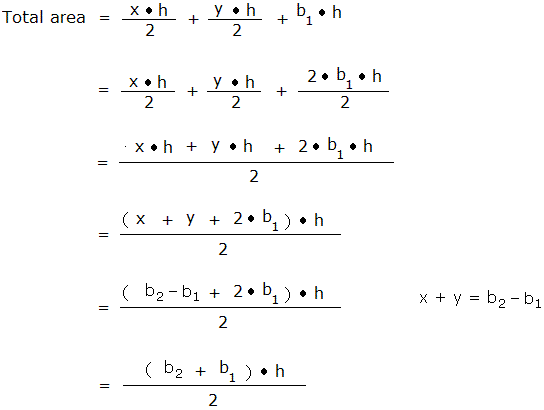The proof of the area of a trapezoid is complete. Any questions, contact me.



sitesforteachers.com Top Sites In Education Teacher-sites-image sitesforparents.com


Page copy protected against web site content infringement by Copyscape








Powered by Site Build It
Copyright © 2008. Basic-mathematics.com. All right reserved