Median of a right isosceles triangle

To show or prove that the median of a right isosceles triangle is half the hypotenuse, start with a right triangle and then draw the median (shown in red in the triangle below)

First, show that triangle ABD and triangle ADC are congruent. If we can show this, then we can conclude that angle BAD and angle DAC are congruent and each is equal to 45 degrees.

This will also mean that angle BDA = 90 degrees.

Therefore, we can use the Pythagorean Theorem for triangle ABC and triangle ABD.

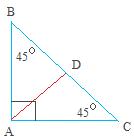
How to show that the right isosceles triangle above (ABC) has two congruent triangles ( ABD and ADC)

Let us show that triangle ABD and triangle ADC are congruent by SSS. This means that we need to find three sides that are equal and we are done.

We already know that segment AB = segment AC since triangle ABC is isosceles.

Since segment AD is the median of segment BC, segment BD = segment DC.

Finally, segment AD is a common side, so it is equal for both triangles.

We have found 3 equal sides, so triangle ABD and triangle ADC are congruent. Since triangle ABD and triangle ADC are congruent, we can do the aforementioned.

Now, let's use the Pythagorean Theorem for triangle ABC and triangle and triangle ABD. The focus now will be on lengths of sides.


For triangle ABC,

x² = y² + y²

x² = 2y²

Divide both sides of the equation by 2

y² = (x²) / 2

For triangle ABD, y² = z² + (x/2)²

Substitute (x²) / 2 for y²

We get:

(x²) / 2 = z² + (x/2)²

(x²) / 2 = z² + (x²) / 4

Subtract (x²) / 4 from both sides of the equation

(x²) / 2 - (x²) / 4 = z² + (x²) / 4 - (x²) / 4

(x²) / 2 - (x²) / 4 = z²

(2x²) / 4 - (x²) / 4 = z²

(x²) / 4 = z²

x/2 = z (Done!)



Learn much more than a right isosceles triangle. Buy a comprehensive geometric formulas ebook. All geometric formulas are explained with well selected word problems