Solve by completing the square
Solve by completing the square could take a little bit more time to do than solving by factoring. Keep reading to see a step-by-step explanation.
Before showing how to solve a quadratic equation by completing the square, you need to understand what a perfect square trinomial is and how to complete a square.
Perfect square trinomial = Binomial × same Binomial
Examples
(x + 4) × (x + 4) = x2 + 4x + 4x + 16 = x2 + 8x + 16 and x2 + 8x + 16 is a perfect square trinomial
(x + a) × (x + a) = x2 + ax + ax + a2 = x2 + 2ax + a2 and x2 + 2ax + a2 is a perfect square trinomial.
How to complete a square by making an important observation
What is the relationship between the coefficient of the second term and the last term?
For x2 + 8x + 16, the coefficient of the second term is 8 and the last term is 16
(8/2)2 = 42 = 16
For, x2 + 2ax + a2, the coefficient of the second term is 2a and the last term is a2
(2a/2)2 = a2
So, what is the relationship?
The last term is obtained by dividing the coefficient of the second term by 2 and squaring the result.
In general, suppose x2 + bx is a binomial. You can complete the square by looking for a perfect square trinomial x2 + bx + c such that c = (b/2)2
Now, let's say you have x2 + 20x and you want to find the last term to make the whole thing a perfect square trinomial.
Just do (20/2)2 = 102. The perfect square trinomial is x2 + 20x + 102 = (x + 10) × (x + 10)
Examples showing how to solve by completing the square.
The steps to follow are straightforward as you can see in the example shown below.
Example #1:
Solve by completing the square x2 + 6x + 8 = 0
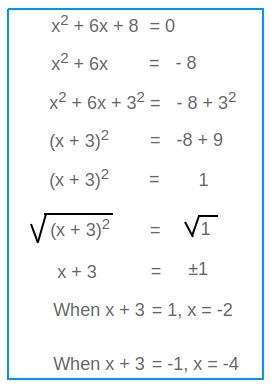
Step-by-Step Explanations
x2 + 6x + 8 = 0
Subtract 8 from both sides of the equation so that you can isolate the two terms containing variables.
x2 + 6x + 8 - 8 = 0 - 8
x2 + 6x = - 8
To complete the square, always do the following 24 hours a day 365 days a year. It is never going to change when you solve by completing the square!
You are basically looking for a term to add to x2 + 6x that will make it a perfect square trinomial.
To this end, get the coefficient of the second term, divide it by 2 and raise it to the second power.
The second term is 6x and the coefficient is 6.
6/2 = 3 and after squaring 3, we get 32
Now, sometimes students forget to do this correctly. You need to add 32 not only to the left side of the equation, but also to the right side of the equation.
x2 + 6x = - 8
Add 32 to both sides of the equation above
x2 + 6x + 32 = - 8 + 32
(x + 3)2 = -8 + 9
(x + 3)2 = 1
Take the square root of both sides so you end up with the linear equations.
√((x + 3)2) = √(1)
x + 3 = ±1
When x + 3 = 1, x = -2
When x + 3 = -1, x = -4
More examples showing how to solve by completing the square
Example #2:
Solve by completing the square x2 + -6x + 8 = 0 instead of x2 + 6x + 8 = 0
The second term this time is -6x and the coefficient is -6.
-6/2 = -3 and after squaring -3, we get (-3)2 = 9
x2 + -6x = - 8
Add (-3)2 to both sides of the equation above
x2 + -6x + (-3)2 = - 8 + (-3)2
(x + -3)2 = -8 + 9
(x + -3)2 = 1
Take the square root of both sides
√((x + -3)2) = √(1)
x + -3 = ±1
When x + -3 = 1, x = 4
When x + -3 = -1, x = 2
Example #3:
Solve by completing the square 3x2 + 8x + -3 = 0
3x2 + 8x + -3 = 0
Divide everything by 3. Always do that when the coefficient of the first term is not 1.
(3/3)x2+ (8/3)x + -3/3 = 0/3
x2+ (8/3)x + -1 = 0
Add 1 to both sides of the equation.
x2 + (8/3)x + -1 + 1 = 0 + 1
x2 + (8/3)x = 1
The second term is (8/3)x and the coefficient is 8/3.
8/3 ÷ 2 = 8/3 × 1/2 = 8/6 and after squaring 8/6, we get (8/6)2
x2 + (8/3)x = 1
Add (8/6)2 to both sides of the equation above
x2 + (8/3)x + (8/6)2 = 1 + (8/6)2
(x + 8/6)2 = 1 + 64/36
(x + 8/6)2 = 36/36 + 64/36 = (36 + 64)/36 = 100/36
Take the square root of both sides
√((x + 8/6)2) = √(100/36)
x + 8/6 = ±10/6
x + 8/6 = 10/6
x = 10/6 - 8/6 = 2/6 = 1/3
x + 8/6 = - 10/6
x = -10/6 - 8/6 = -18/6 = -3
To solve by completing the square can become quickly hard as shown in example #3
Recent Articles
-
Fundamental Counting Principle
Jun 06, 23 07:32 AM
The fundamental counting principle is introduced in this lesson. Learn how to count with the multiplication principle and the addition principle. -
45-45-90 Triangle
May 01, 23 07:00 AM
What is a 45-45-90 triangle? Definition, proof, area, and easy to follow real-world examples.
100 Tough Algebra Word Problems.
If you can solve these problems with no help, you must be a genius!
