Solving quadratic equations by factoring

Solving quadratic equations by factoring could be many times the simplest and quickest way to solve quadratic equations as long as you know how to factor. I strongly recommend that you study or review the following important unit about factoring.

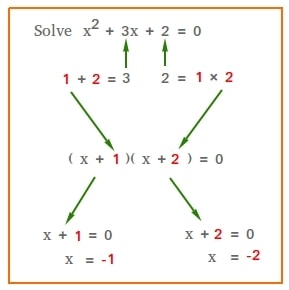
Example #1:  It explains in more details how to solve x² + 3x + 2 = 0 or the example in the figure above.

Solve x² + 3x + 2 = 0

First, you have to factor x² + 3x + 2

Since the coefficient of x² is 1 (x² = 1x²), you can factor by looking for factors of the last term (last term is 2) that add up to the coefficient of the second term (3x, coefficient is 3)

2 = 1 × 2

2 = -1 × -2

1 + 2 = 3 and 3 is the coefficient of the second term.

x² + 3x + 2 = ( x + 2) × ( x + 1)

x² + 3x + 2 = 0 gives ( x + 2) × ( x + 1) = 0

( x + 2) × ( x + 1) = 0 when either x + 2 = 0 or x + 1 = 0

x + 2 = 0 when x = -2

x + 1 = 0 when x = -1

Let us now check x = -2 and x = -1 are indeed solutions of x² + 3x + 2 = 0

(-2)² + 3 × -2 + 2 = 4 + -6 + 2 = 3 + -6 = 0

(-1)² + 3 × -1 + 2 = 1 + -3 + 2 = 3 + -3 = 0


If instead you were solving x² + -3x + 2 = 0, you will use -1 and -2 since -1 + - 2 add up to -3.

( x + -2) × ( x + -1) = 0

( x + -2) × ( x + -1) = 0 when either x + -2 = 0 or x + -1 = 0

x + -2 = 0 when x = 2

x + -1 = 0 when x = 1

Check that 1 and 2 are indeed the solutions

Tougher examples of solving quadratic equations by factoring.

Example #2: Solving quadratic equations by factoring

Solve x² + x + -30 = 0

First, you have to factor x² + x + -30

-30 = 30 × -1

-30 = 15 × -2

-30 = 6 × -5

-30 = -30 × 1

-30 = -15 × 2

-30 = -6 × 5

Since only 6 + -5 = 1, and 1 is the coefficient of the second term(x = 1x), x² + x -30 = ( x + 6) × ( x - 5)

x² + x + -30 = 0 gives ( x + 6) × ( x - 5) = 0

( x + 6) × ( x - 5) = 0 when either x + 6 = 0 or x - 5 = 0

x + 6 = 0 when x = -6

x - 5 = 0 when x = 5

Let us now check x = -6 and x = 5 are indeed solutions of x² + x + -30 = 0

(-6)² + -6 -30 = 36 - 6 - 30 = 30 - 30 = 0

(5)² + 5 - 30 = 25 + 5 - 30 = 30 - 30 = 0


If instead you were solving x² + -x + -30 = 0, you will use -6 and 5 since -6 + 5 = -1

x² + -x - 30 = 0


( x - 6) × ( x + 5) = 0

( x - 6) × ( x + 5) = 0 when either x - 6 = 0 or x + 5 = 0

x - 6 = 0 when x = 6

x + 5 = 0 when x = -5

Check that 6 and -5 are indeed the solutions

Solving quadratic equations by factoring can get very tough. See below:

Example #3: Solving quadratic equations by factoring

6x² + 27x + 30 = 0

First factor 6x² + 27x + 30

6x² + 27x + 30 = ( 3x + ?) × (2x + ?) or ( 6x + ?) × (x + ?)

Now, factor the last term 30

30 = 30 × 1

30 = 15 × 2

30 = 6 × 5

To get the 27x, you have to try out the cross multiplications below. There are 6 of them. Cross multiply and add!

6x         x
30         1

6x + 30x = 36x

6x         x
15         2

12x + 15x = 27x

6x         x
6          5

30x + 6x = 36x

3x         2x
30         1

3x + 60x = 63x

3x         2x
15         2

6x + 30x = 36x

3x         2x
6           5

15x + 12x = 27x

You got a couple of choices shown in bold!

6x² + 27x + 30 = 0

(6x + 15) × ( x + 2)= 0

6x + 15 = 0

6x = -15

x = -15/6

x + 2 = 0

x = -2