Surface area of a rectangular prism

To derive the formula of the surface area of a rectangular prism, follow closely the steps below. Start with a right rectangular prism as shown below and call the length l, the width w, and the height h.

In order to make a rectangular prism like the one shown above, you basically use the following rectangular prism template:

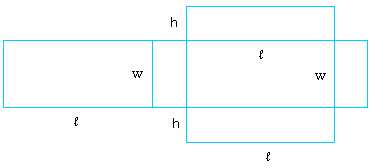
Looking at the rectangular prism template, it is easy to see that the solid has six sides and each side is a rectangle.

The bottom side and the top side are equal and have l and w as dimensions.

The area for the top and bottom sides is l × w + l × w = 2 × l × w

The front side (shown in sky blue) and the back side (not shown) are equal and have h and l as dimensions.

The area for the front and the back sides is l × h + l × h = 2 × l × h

Then, the left and right sides have h and w as its dimensions. One side is shown in purple.

The area for the left and the right sides is w × h + w × h = 2 × w × h
The total surface area, call it SA is:

SA = 2 × l × w   +   2 × l × h  +  2 × w × h

Examples showing how to find the surface area of a rectangular prism

Example #1:

Find the surface area of a rectangular prism with a length of 6 cm, a width of 4 cm, and a height of 2 cm.

SA = 2 × l × w  +  2 × l × h  +  2 × w × h

SA = 2 × 6 × 4  +  2 × 6 × 2  +  2 × 4 × 2

SA = 48 + 24 + 16

SA = 88 cm²


Example #2:

Find the surface area of a rectangular prism with a length of 4 cm, a width of 5 cm, and a height of 10 cm.

SA = 2 × l × w  +  2 × l × h  +  2 × w × h

SA = 2 × 4 × 5  +  2 × 4 × 10  +  2 × 5 × 10

SA = 40 + 80 + 100

SA = 220 cm²


Example #3:

Find the surface area with a length of 1/2 cm, a width of 8 cm, and a height of 1/4 cm.

SA = 2 × l × w  +  2 × l × h  +  2 × w × h

SA = 2 × 1/2 × 8  +  2 × 1/2 × 1/4  +  2 × 8 × 1/4

SA = 1 × 8  +  1 × 1/4  +  16 × 1/4

SA = 8 + 1/4 + 4

SA = 12 + 1/4

SA = 48/4 + 1/4

SA = 49/4 cm²

SA = 12.25 cm²