The sine ratio

To help you understand what the sine ratio is, we will do an activity that is similar to the one we did for the tangent ratio.

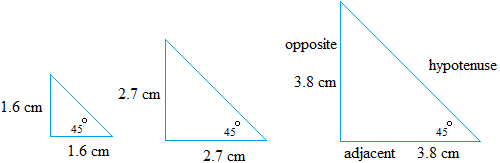
In the lesson about tangent ratio, we used these triangles to find the tangent ratio.

Instead of doing ratios of opposite to adjacent, what if we did ratios of opposite to hypotenuse? Let us try that. To get the value of the hypotenuse, you have two choices.

You could use the pythagorean theorem or measure the lengths with a ruler. 

I measured with a ruler and found the following lengths. Keep in mind that these measurements are not perfect and that is not the point.

Triangle on the left: 2.24 cm

Triangle in the middle: 3.8 cm

Triangle on the right: 5.3 cm

Notice that the ratio is closely equal to 0.71 cm no matter the size of the triangles. 

A more straightforward way to find the sine ratio.

There is a way to find a more accurate value for the sine ratio. Since the size of the triangle does not matter, you could use a value of 1 for the opposite and adjacent side.

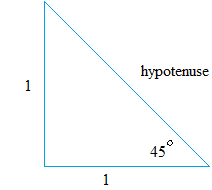
We use the pythagorean theorem this time to find the length of the hypotenuse

hypotenuse² = 1² + 1²

hypotenuse² = 1 + 1

hypotenuse² = 2

hypotenuse = √ 2



As you can see, what we got here is closely equal to the values we found before.

Whenever the ratio is found by using the opposite side and the hypotenuse, we call it sine ratio instead of tangent ratio.

We then say that sine 45 degrees is equal to 0.707. In short, we can use the symbol sin instead of sine and write sin (45 degrees) = 0.707 

Cosine ratio

When you do a ratio of adjacent to hypotenuse, this ratio is called the cosine ratio.

Take a look again at the triangles. You will see that the adjacent side has the same value as the opposite side. 

This means that the cosine of 45 degrees is the same as the sine of 45 degrees.

You can use the symbol cos instead of cosine and write cos (45 degrees) = 0.707