Union of sets
This lesson will explain how to find the union of sets. We will start with a definition of the union of two sets.
Definition: Given two sets A and B, the union of sets A and B is the set that contains elements or objects that belong to either A or to B or to both.
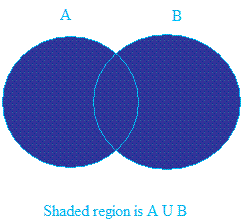
We write A ∪ B and A ∪ B is read as A union B.
Basically, we find A ∪ B by putting all the elements of A and B together. We next illustrate with examples.
Example #1
Let A = {1 orange, 1 pineapple, 1 banana, 1 apple} and B = {1 spoon, 1 knife, 1 fork}
A ∪ B = {1 orange, 1 pineapple, 1 banana, 1 apple, 1 spoon, 1 knife, 1 fork}
Example #2
Find the union of A and B
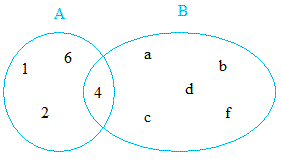
A = {1, 2, 4, 6} and B = {4, a, b, c, d, f}
A ∪ B = {1, 2, 4, 6, 4, a, b, c, d, f} = {1, 2, 4, 6, a, b, c, d, f}
Notice that it is perfectly OK to write 4 once or twice.
Example #3
A = {x / x is a number bigger than 4 and smaller than 8}
B = {x / x is a positive number smaller than 7}
A = {5, 6, 7} and B = {1, 2, 3, 4, 5, 6}
A ∪ B = {1, 2, 3, 4, 5, 6, 7}
Or A ∪ B = { x / x is a number bigger than 0 and smaller than 8}
Again, notice that 5 and 6 were written only once although it would be perfectly OK to write them twice.
Example #4
A = {x / x is a country in Asia}
B = {x / x is a country in Africa}
A ∪ B = {x / x is a country in Asia and Africa} = {all countries in Asia and Africa}
Technically, using the definition, we should have said A ∪ B = {x / x is a country in either Asia or Africa or both countries}
However, in real life, this is not the way we talk. By saying all countries in Asia and Africa, it is usually understood in daily conversations that we are talking about all countries in Asia and all countries in Africa.
Example #5
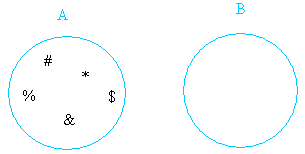
A = {#, %, &, * , $ }
B = { }
A ∪ B = {#, %, &,* , $}
Notice that B is the empty set also called the null set . The union of any set with the empty set is the set itself.
You may have definitely noticed that the union of sets is simply found by putting the elements of the sets together, preferably without repetition.
Definition of the union of three sets
Given three sets A, B, and C the union is the set that contains elements or objects that belong to either A, B, or to C or to all three.
We write A ∪ B ∪ C
Basically, we find A ∪ B ∪ C by putting all the elements of A, B, and C together.
A = {1, 2, 4, 6}, B = {a, b, c,} and C = A = {#, %, &, * , $}
A ∪ B ∪ C = {1, 2, 4, 6, a, b, c,#, %, &, * , $}
The first graph in the beginning of this lesson shows the shaded region for the union of two sets.
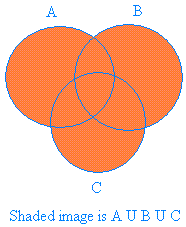
The graph below shows the shaded region for the union of three sets.
Properties of the union of sets
Commutative law
A ∪ B = B ∪ A
Example
A = {a, b, c, d}
B = {e, f, g}
A ∪ B = {a, b, c, d, e, f, g}
B ∪ A = {a, b, c, d, e, f, g}
Associative law
(A ∪ B) ∪ C = A ∪ (B ∪ C)
Example
A = {a, b, c, d}
B = {e, f, g}
C = {h, i}
A ∪ B = {a, b, c, d, e, f, g}
(A ∪ B) ∪ C = {a, b, c, d, e, f, g} ∪ {h, i}
(A ∪ B) ∪ C = {a, b, c, d, e, f, g, h, i}
B ∪ C = {e, f, g} ∪ {h, i} = {e, f, g, h, i}
A ∪ (B ∪ C) = {a, b, c, d} ∪ {e, f, g, h, i}
A ∪ (B ∪ C) = {a, b, c, d, e, f, g, h, i}
Idempotent law
A ∪ A = A
Example
A = {x, y, z}
A ∪ A = {x, y, z} ∪ {x, y, z}
A ∪ A = {x, y, z}
Again, there is no need to repeat elements that are in both sets. That is the reason we also say that the union of sets is the smallest set that contains all the elements of all the sets.
Identity Law
Let ∅ or { } be the empty set
A ∪ ∅ = A
Example
A = {Maserati, BMW, Mercedes}
A ∪ ∅ = {Maserati, BMW, Mercedes} ∪ { }
A ∪ ∅ = {Maserati, BMW, Mercedes}
Domination Law
Let U be the universal set or the set that contains elements.
A ∪ U = U
A = {0, 1, 2}
U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
A ∪ U = {0, 1, 2} ∪ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
A ∪ U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
This ends the lesson about union of sets. If you have any questions about the union of sets, I will be more than happy to answer them.

