Method of Comparing Decimals

Interactive Lesson to Compare two Decimals

How to Compare Decimals

Comparing decimals is a pretty straightforward concept. We will teach you how to do it here with ease.

First, compare the whole numbers to the left of the decimal point. If they are not the same, the smaller decimal number is the one with the smaller whole number.

For instance, compare 52.432 with 45.989

52 is bigger than 45, so the bigger decimal number is 52.432

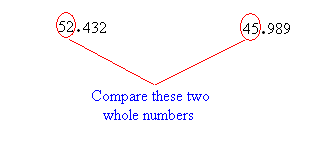
We write 52.432 > 45.989 or 45.989 < 52.989

On the other hand, if they are the same, compare the whole number to the right of the decimal point.

The smaller decimal number is the one with the smaller whole number on the right of the decimal point.

for instance, compare 60.802 with 60.504

The whole numbers to the left of the decimal point are equal, so compare the whole numbers to the right of the decimal point.

504 is smaller than 802, so the smaller decimal number is 60.504.

We write 60.504 < 60.802 or 60.802 > 60.504

Sometimes, they may not have the same number of decimal places to the right of the decimal point.

Just add zero(s) in this case!

For instance, compare 10.598 with 10.61

add a 0 after 61 to get 10.610

610 is bigger than 598, so 10.598 < 10.61

Other examples:

4.7 > 4.4

3.23 < 3.25

7.34 < 7.304

Other times, it may not be obvious which one of the whole numbers to the right of the decimal point is bigger or smaller.

In this case, compare each digit to the right of the decimal point starting with the tenths place

If the digits in the tenths place are equal, compare the digits in the hundredths place, and so forth...

for instance, compare 0.043 with 0.00985


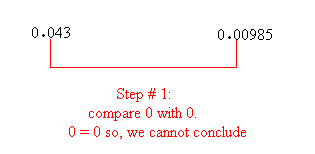
Compare 1.2045 with 1.2050

The digits in the tenths place, which are 2 and 2 are equal, so we cannot conclude.

The digits in the hundredths place, which are 0 and 0 are equal, so we cannot conclude

The digits in the thousandths place are 4 and 5.

4 < 5, so 1.2045 < 1.2050

Comparing decimals quiz. See how well you can compare decimals.