Algebra proofs

Many algebra proofs are done using proof by mathematical induction. To demonstrate the power of mathematical induction, we shall prove an algebraic equation and a geometric formula with induction.

If you are not familiar with with proofs using induction, carefully study proof by mathematical induction given as a reference above. Otherwise, you could struggle with these algebra proofs below

Algebra equation:

Prove by mathematical induction that 1 + 2 + 4 + 8 + ... + 2^n-1 = 2ⁿ - 1

Step # 1:

Show that the equation is true for n = 2. n = 2 means adding the first two terms

1 + 2 = 3 and 2² - 1 = 4 - 1 = 3. So, it is true for n =2

Just for fun, let's show it is true also for n = 4. n =4 means adding the first 4 terms

1 + 2 + 4 + 8 = 15 and 2⁴ - 1 = 16 - 1 = 15. So, it is true also for n =4

Step # 2:

Suppose it is true for n = k

Just replace n by k

1 + 2 + 4 + 8 + ... + 2^k-1 = 2^k - 1

Step # 3:

Prove it is true for n = k + 1

You need to write down what it means for the equation to be true for n = k + 1

Caution: Writing down what it means is not the same as proving the equation is true. In fact, it just shows you what you need to prove

Here is what it means for n = k + 1:

After you replace k by k+1, you get :

1 + 2 + 4 + 8 + ... + 2^{k + 1 -1} = 2^{k + 1} - 1

1 + 2 + 4 + 8 + ... + 2^k = 2^{k + 1} - 1

You can now complete the proof by using the hypothesis in step # 2 and then show that

1 + 2 + 4 + 8 + ... + 2^k = 2^{k + 1} - 1

starting with the hypothesis, 1 + 2 + 4 + 8 + ... + 2^k-1 = 2^k - 1

ask yourself, " What does the next term look like? "

Since the last term now is 2^k-1, the next term should be 2^{k + 1 -1} = 2^k after replacing k by k + 1

Add 2^k to both sides of the hypothesis

1 + 2 + 4 + 8 + ... + 2^k-1 + 2^k = 2^k - 1 + 2^k

The trick here is to see that 2^k + 2^k = 2 × 2^k = 2¹× 2^k = 2^{k + 1}

1 + 2 + 4 + 8 + ... + 2^k-1 + 2^k = 2^k - 1 + 2^k

                                             = 2 × 2^k -1

                                             = 2¹× 2^k -1

                                             = 2^{k + 1} -1

Geometric formula:

Show by mathematical induction that

the sum of the angles in an n-gon = ( n - 2 ) × 180^°

A couple of good observations before we prove it:

Observation #1:

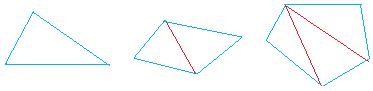
An n-gon is a closed figure with n sides. For example,

an n-gon with 4 sides is called a quadrilateral

an n-gon with 3 sides is called a triangle

Observation #2:

After a close examination of the figure above, can you see that every time you add a side, you are also adding one more triangle

I am now ready to show the proof.

Step # 1:

Show that the equation is true for n = 3. Notice that n cannot be smaller than 3 since we cannot make a closed figure with just two sides or one side.

When n = 3, we get a triangle and the sum of the angles in a triangle is equal to 180^°

When n = 3, ( 3 - 2 ) × 180^° = 1 × 180^° = 180^°

When n = 4, you are adding one more triangle to get two triangles and the sum of the angles of the two triangles is equal to 360^°

When n = 4, ( 4 - 2 ) × 180^° = 2 × 180^° = 360^°

Thus, the formula is true for n = 3 and n = 4

Step # 2:

Suppose it is true for n = k

Just replace n by k

The sum of the angles in a k-gon = ( k - 2 ) × 180^°

Step # 3:

Prove it is true for n = k + 1

You need to write down what it means for the equation to be true for n = k + 1

Here is what it means for n = k + 1:

After you replace k by k+1, you get :

The sum of the angles in a (k+1)-gon = ( k +1 - 2 ) × 180^°

The sum of the angles in a (k+1)-gon = ( k - 1 ) × 180^°

You can now complete the proof by using the hypothesis in step # 2 and then show that

The sum of the angles in a (k+1)-gon = ( k - 1 ) × 180^°

starting with the hypothesis, the sum of the angles in a k-gon = ( k - 2 ) × 180^°

ask yourself, " What does the next term look like? "

Since the last term now is k-gon or a figure with k sides, the next term should be a figure with k + 1 sides after replacing k by k + 1

Now, what are we adding to both sides?

First, recall the meaning of adding one side. It means that you will be adding also one triangle

( k + 1) gon = k-gon + ( 1 side or one more triangle)

( k + 1) gon = k-gon + one more triangle

( k + 1) gon = k-gon + 180^°

So add 180^° to both sides of the hypothesis

The sum of the angles in a k-gon + 180^° = ( k - 2 ) × 180^° + 180^°

The sum of the angles in a (k+1)-gon = ( k - 2 ) × 180^° + 180^°

                                             = 180^°k + -2 × 180^° + 180^°

                                             = 180^°k + -1 × 180^°

                                             = 180^° ( k + -1 )