Lattice method for multiplication

Although the lattice method for multiplication is no longer being used right now in school, it is quite easy understand.

I will illustrate with two good examples. Study them carefully and follow the steps exactly as shown.

Example #1:

Multiply 42 and 35

Arrange 42 and 35 around a 2 × 2 grid as shown below:

Draw the diagonals of the small squares as shown below:

Multiply 3 by 4 to get 12 and put 12 in intersection of the first row and the first column as show below.

Notice that 3 is located in the first row and 4 in the first column. That is why the answer goes in the intersection.

By the same token, multiply 5 and 2 and put the answer in the intersection of second row and the second column.

And so forth...

Then, going from right to left, add the numbers down the diagonals as indicated with the arrows.

The first diagonal has only 0. Bring zero down.

The second diagonal has 6, 1, 0. Add these numbers to get 7 and bring it down.

And so forth...

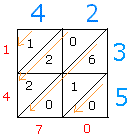
After the grid is completed, what you see in red is the answer that is 1470.

Another example showing how the lattice method for multiplication works

Example #2:

Multiply 658 and 47

Arrange 657 and 47 around a 3 × 2 grid as shown below:


Draw the diagonals of the small squares, find products, and put the answers in intersecting rows and columns as already demonstrated:


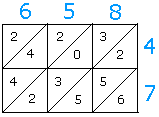
Then, going from right to left, add the numbers down the diagonals as shown before.

The first diagonal has only 6. Bring 6 down.

The second diagonal has 2, 5, and 5. Add these numbers to get 12. Bring 2 down and carry the 1 over to the next diagonal.

The third diagonal has 3, 0, 3, and 2. Add these numbers to get 8 and add 1 (your carry) to 8 to get 9.

and so forth...

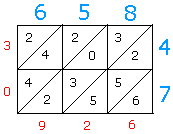
After the grid is completed, what you see in red is the answer to the multiplication that is 30926.

I understand that this may be your first encounter with the lattice method for multiplication. It may seem that it is tough. Just practice with other examples and you will be fine.

Any questions about the lattice method for multiplication? Just contact me.