Pythagorean theorem word problems

Pythagorean theorem word problems arise in numerous situations. We will cover a few solid examples here. 

Pythagorean problem # 1

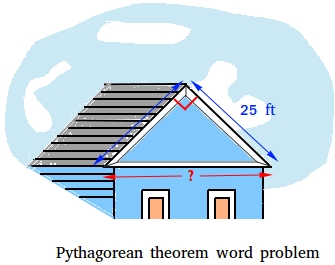
The diagram below shows the roof of a house. Suppose you need to replace a beam that connects the two sides of the roof. How long should be beam be?

The beam is the horizontal line and its length is shown with a red line. Notice that the sides of the roof have the same length. Furthermore, since the two sides of the roof make a right triangle, we can use the Pythagorean theorem to find the length of the beam.

c² = a² + b²

c² = 25² + 25²

c² = 625 + 625

c² = 1250

c = √1250 = 35.35

The length of the beam is 35.35 feet.

More interesting Pythagorean theorem word problems

Pythagorean problem # 2

John leaves school to go home. He walks 6 blocks North and then 8 blocks west. How far is John from the school? Here is how you can model this situation.



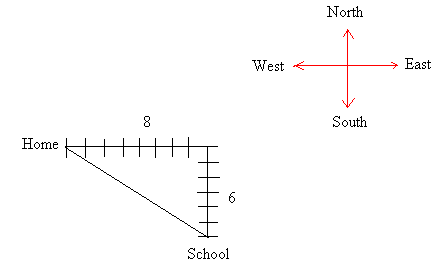
The distance from school to home is the length of the hypotenuse.

Let c be the missing distance from school to home and a = 6 and b = 8

c² = a² + b²

c² = 6² + 8²

c² = 36 + 64

c² = 100

c = √100

c = 10

The distance from school to home is 10 blocks.

Pythagorean problem # 3

A 13 feet ladder is placed 5 feet away from a wall. The distance from the ground straight up to the top of the wall is 13 feet. Will the ladder reach the top of the wall?



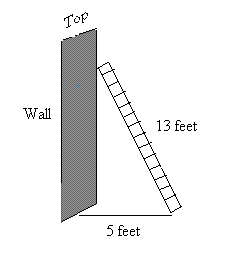
Let the length of the ladder represents the length of the hypotenuse or c = 13 and a = 5 the distance from the ladder to the wall.

c² = a² + b²

13² = 5² + b²

169 = 25 + b²

169 - 25 = 25 - 25 + b² (minus 25 from both sides to isolate b² )

144 = 0 + b²

144 = b²

b = √144 = 12

The ladder will never reach the top since it will only reach 12 feet high from the ground yet the top is 13 feet high.