Scientific notation
Scientific notation is a convenient way to deal with very large or very small numbers.
It provides an easier way to write numbers and make multiplication and division of very large or very small numbers a lot easier.
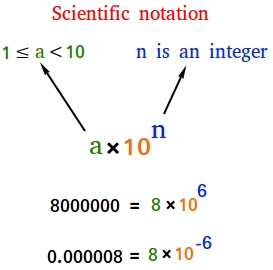
A number is in this format if we can write it as:
a × 10n
with 1 ≤ a < 10 and n is an integer.
1 ≤ a < 10 means that a is a number between 1 and 10
Thus, a can be 1,2,3,4,5,6,7,8, and 9
Let's start with something simple.Write 500 in this useful notation:
500 = 5 × 100 = 5 × 102
You can also claim as we saw before that there is a decimal point after 0 and write 500.0
Then, move the decimal point 2 places to the left between 5 and 0 to get 5.000, which is the same as 5.
Since you moved it two places to the left, you know that your exponent is 2.
Your base is always 10
Thus, 500 = 5 × 102
More examples:
1) 75000
75000 = 75000.0
Move the decimal point 4 places to the left between 7 and 5.
We get 7.5000, which is the same as 7.5
Since we moved it 4 places to the left, your exponent is 4 and your base is still 10.
Thus, 75000 = 7.5 × 104
Sometimes, instead of moving your decimal point to the left, you have to move it to the right as the following example demonstrates:
When you move your decimal point to the right, your exponent is negative.
2) 0.002
Move your decimal point 3 places to the right after the 2 to get 0002. and 0002. is the same as 2. or 2
Since you had to move it 3 places to the right, your exponent is -3 and the base is still 10
Thus, 0.002 = 2 × 10-3
3) 0.000065
Move decimal point 5 places to the right
The answer is 6.5 × 10-5
4) 650000
Move decimal point 5 places to the left
The answer is 6.5 × 105
Exponents
Laws of Exponents
Scientific notation
Home page
|
