Set Notation
The different ways to write or define a set is called set notation. However, what is a set? Let us start with a definition of a set.
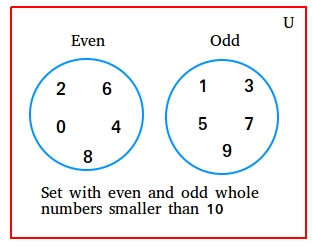
Basically, anything with a collection of objects is a set. Here is an example of set made with odd and even whole numbers less than 10.
You may now feel that you could easily make up our own sets.You could be surprised what a set could be made of. Basically, any collections of things that make sense.
This figure shows the set of even and odd whole number smaller than 10.
1. The set of all letters in the modern English alphabet.
What is included in that set? a, b, c, d, e, f, etc...
2. The set of all great mathematicians in the past.
What is included in that set? We could mention names such as Carl Gauss, Isaac Newton, Einstein, Blaise Pascal, Euclid, Pierre de Fermat, etc...
3. The set of all positive numbers less than 10.
What is included in that set? 1, 2, 3, 4, 5, 6, 7, 8, 9
4. The set of all types of sausages.
What is included in that set? I am not sure since I am knowledgeable enough in this area. I know Italian sausage and ???. What else? Did I miss something?
5. The set of all states in the United States.
Oh boy. Geography! You know what? I think you got the point. Let us now explain what a set notation is.
Set notation or ways to define a set
a. You could define a set with a verbal description: All sets above are described verbally when we say, " The set of all bla bla bla "
b. You could make a listing of all members separated by commas with braces { and }: A list of set 1. is written as: {a, b,c,d,e,f,....,z}
c. Set-builder notation:
Set 1 and set 4 can be written as { x / x is a letter of the modern English alphabet} and { x / x is a type of sausage}
{ x / x is a letter of the modern English alphabet} is read, " The set of all x such that x is a letter in the modern English alphabet.
Set-builder is an important concept in set notation. You must understand it!
We use capital letters such as A, B, and so forth to denote sets.
For example, you could let A be the set of all positive numbers less than 10.
We use the symbol ∈ to indicate that an object belongs to a set and the symbol ∉ to indicate that an object does not belong to a set.For example, if A is the set of all positive numbers less than 10, then 2 ∈ A, but 12 ∉ A
A set that has no element is called empty set and is denoted by { } or ∅
For example, {x / x is a human being who have lived 10,000 years} is an empty set because it is impossible to find at least one human being who have lived so long.
Two sets are equal if they have exactly the same elements.
For example, { x / x is a number between bigger than 1 and less than 5} and { 2, 3, 4} are equal sets.
Subtleties with set notation.
Two sets are still equal even if the same element is listed twice{ 2, 3, 4} and { 2, 3, 3, 4} are equal
The order of elements in sets does not matter
{ 2, 3, 4} = { 2, 3, 3, 4} = { 4, 3, 2}
Finite and infinite set:
A set is finite if you can list all its elements and infinite otherwise.
All sets described above are finite because you can list or count all their elements.
However, among the five sets, one set can be turned into an infinite set with one small change. That set is set number 3.
If I get rid of the word positive and say instead "the set of all numbers less than 10" the set in now infinite because you cannot count all those numbers less than 10.