Special right triangles

There are two types of special right triangles. The first type is the 45°- 45°- 90° triangle and the second type is the 30°- 60°- 90° triangle.
The 45°- 45°- 90° triangle is an isosceles right triangle and the 30°- 60°- 90° triangle is a scalene right triangle.

The 450 - 450 - 900 triangle:

In this triangle, the important thing to remember is that the legs have equal length.

Let's call the longest side hypotenuse. Using the Pythagorean theorem, we get: 

45-45-90 degrees special right triangle
Hypotenuse2 = Leg2 + Leg2

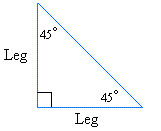
Hypotenuse2 = 2×Leg2

Let's take the square root of both sides

√(Hypotenuse2) = √(2×Leg2)

Hypotenuse = √(2)×√(Leg2)

So, the formula is:

Hypotenuse = √(2)×(Leg)

 Now, what's the point of having a formula like that? Well, it is a shortcut to solve problems.

If the legs of a right triangle are equal, you can quickly find the length of a leg if the length of the hypotenuse is given or you can find the length of the hypotenuse if the length of a leg is given.

The 300 - 600 - 900 triangle:

30-60-90 degrees special right triangle
Since the short leg is 1/2 the hypotenuse, the hypotenuse is 2 × short leg.

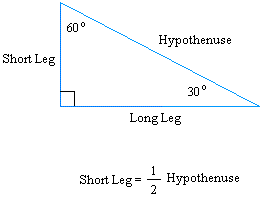
Using the Pythagorean theorem, we get:

Hypotenuse2 = (Short Leg)2 + (Long Leg)2

(2 × Short Leg)2 = (Short Leg)2 + (Long Leg)2

(2 × Short Leg)×(2 × Short Leg) = (Short Leg)2 + (Long Leg)2

(4 × (Short Leg)2) = (Short Leg)2 + (Long Leg)2

4 × (Short Leg)2 − (Short Leg)2 = (Short Leg)2 − (Short Leg)2 + (Long Leg)2

4 × (Short Leg)2 − (Short Leg)2 = 0 + (Long Leg)2

4 × (Short Leg)2 − (Short Leg)2 = (Long Leg)2

3 × (Short Leg)2 = (Long Leg)2

Let's take the square root of both sides

√(3 × Short Leg2) = √((Long Leg)2)

(√3) × √((Short Leg)2) = Long Leg

(√3) × (Short Leg) = Long Leg

So, the formula for the long leg is: Long Leg = (√3) × (Short Leg)

 Since the short leg = 1/2(hypotenuse), long Leg is also equal to:

(√3) × 1/2(hypotenuse)

A couple of problems about special right triangles

Example #1:

The legs of an isosceles right triangle measure 10 inches. Find the length of the hypotenuse.

Since the triangle is isosceles, the legs are equal and we can use the formula.

Hypotenuse = √(2)×(Leg)

Hypotenuse = √(2)×(10)= 14.1421 inches

Example #2

The two legs of a right triangle are the same length. The hypotenuse is 4 meters long.

Find the length of the legs. Express your answer in simplified radical form, or as a decimal rounded to four places.

Let x be the length of one leg and let x be the length of the other leg.

x2 + x2 = 42

2x2 = 16

Divide both sides by 2

x2 = 8

x = √(8)

x = √(4 × 2)

x = √(4) × √(2)

x = 2 × √(2)

or

x = 2 × 1.414213

x = 2.828426

x = 2.8284

Notice that you can get the same answer faster if you just use the formula.

Hypotenuse = √(2) × (Leg)

4 = √(2) × Leg

Leg  = 4 / √(2) = 2.8284

Example #3:

The hypotenuse of a 30°-60°-90° triangle is equal to 20 inches. Find the short leg and the long leg.

Short Leg = 1/2 × (hypotenuse) = 1/2 × 20 = 10 inches.

Long leg = (√3) × Short Leg = √3 × 10 = 17.32 inches.

Send me questions here about special right triangles.

Pythagorean theorem