Surface area of a sphere

The surface area of a sphere is the total area of the curved surface of the sphere since the shape of a sphere is completely round.

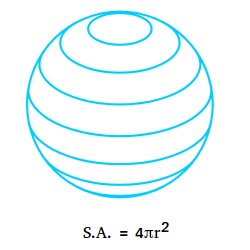
Surface area of a sphere formula

The surface area is expressed in square units.

• If r is measured in feet, then the surface area is measured in square feet or ft².

• If r is measured in centimeters, then the surface area is measured in square centimeters or cm². 

• If r is measured in inches, then the surface area is measured in square inches or in.²

How to derive the formula of the surface area of the sphere

To derive the formula of the surface area of a sphere, we imagine a sphere with many pyramids inside of it until the base of all the pyramids cover the entire surface area of the sphere. In the figure below, only one of such pyramid is shown.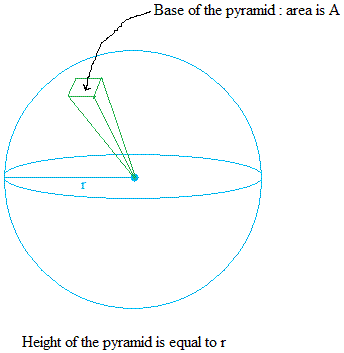

Then, do a ratio of the area of the pyramid to the volume of the pyramid.

The area of the pyramid is A_pyramid.

The volume of the pyramid is V_pyramid = (1/3) × A_pyramid × r = (A_pyramid × r) / 3

Now pay careful attention to the following important stuff!

Observation # 1:

For a large number of pyramids, let's say that n is such a large number, the ratio of the surface area of the sphere to the volume of the sphere is the same as 3 / r.

Why is that? That cannot be true! Well, here is the reason:

For n pyramids, the total surface area is n × A_pyramid

Also for n pyramids, the total volume of the sphere is n × V_pyramid

Therefore, ratio of total surface area of the sphere to total volume of the sphere is

(n × A_pyramid) / (n × V_pyramid)  = A_pyramid / V_pyramid

We have already shown above that A_pyramid / V_pyramid = 3 / r

Therefore, S.A._sphere / V_sphere is also equal to 3 / r.

Observation # 2:

Furthermore, n × A_pyramid = S.A._sphere (The total area of the bases of all pyramids or n pyramids is approximately equal to the surface area of the sphere)


n × V_pyramid = V_sphere ( The total volume of all pyramids or n pyramids is approximately equal to the volume of the sphere.

Using observation #2, do a ratio of S.A._sphere to V_sphere

S.A._sphere / V_sphere = n(A_pyramid) / n(V_pyramid)  

Cancel n 

S.A._sphere / V_sphere = (A_pyramid) / (V_pyramid)

S.A._sphere / V_sphere = 3 / r

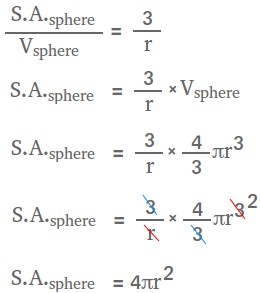
Therefore, the total surface area of a sphere, call it SA is:

SA = 4 × pi × r²

A couple of examples showing how to find the surface area of a sphere.

Example #1:

Find the surface area of a sphere with a radius of 6 cm

SA = 4 × pi × r²

SA = 4 × 3.14 × 6²

SA = 12.56 × 36

SA = 452.16

Surface area = 452.16 cm²

Example #2:

Find the surface area of a sphere with a radius of 2 cm

SA = 4 × pi × r²

SA = 4 × 3.14 × 2²

SA = 12.56 × 4

SA = 50.24

Surface area = 50.24 cm²

How to find the surface area of a hemisphere

The surface area of a hemisphere is the total area of the surface of the hemisphere. The surface of a hemisphere consists of a circular base and the curved surface of the hemisphere. 

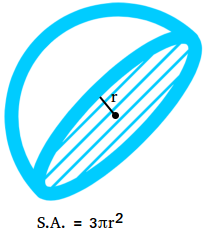
For a hemisphere, the area of the curved surface is half the surface area of the sphere.

Area of the curved surface = (1/2)4πr²

Area of the curved surface = (1/2)4πr²

Area of the curved surface = 2πr²

The area of the circular base is πr²

Surface area of hemisphere = 2πr² + πr²

Surface area of hemisphere = 3πr²

Example #3:

The diameter of a sphere is 8 cm. Find the surface area of the hemisphere.

r = d/2 = 8/2 = 4

Surface area of hemisphere = 3πr² = 3π(4)² = (3)(3.14)(16) = 150.72 cm²

How to find the surface area of a sphere when the volume of a sphere is given in two easy steps

Example #4

The volume of a sphere is 33.5103 cubic units. Find the surface area of the sphere.

Step 1

Use the volume to find the radius of the sphere.

V = (4/3)πr³

33.5103 = (4/3)πr³

33.5103 = (1.3333)(3.14)r³

33.5103 = (4.186562)r³

Divide both sides by 4.186562

33.5103 / 4.186562 = r³

8.004 = r³

r = cube root of 8.004  = 2

Step 2

Use the radius to find the surface area.

S.A. = 4πr²

S.A. = 4(3.14)(2)²

S.A. = (12.56)(4)

S.A. = 50.24 square units