What is the golden ratio?
What is the golden ratio? The short answer is 1.61803398875 and many people call it the divine proportion. The golden ratio was discovered by the Pythagoreans around 500 B.C.
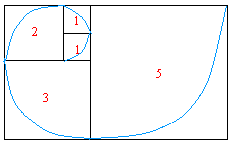
Draw a 1-unit square. Then draw another 1-unit square next to the first.
Attach a 2-unit square( sum of the two previous side lengths) along a matching side length.
Attach a 3-unit square( sum of the two previous side lengths) along a matching side length.
Attach a 5-unit square( sum of the two previous side lengths) along a matching side length.
Finally, using the side length of each square as the radius, draw a quarter-circle arc in each square. All arcs should be connected.
So far, you should get something that looks like the figure above:
Feel free to continue adding squares to the guide.
If you do, the square should have the following side lengths: 8, 13, 21, .....
The lengths of all squares will give a Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, 21, ...etc, ...
If the quotient of each consecutive pair of numbers is formed ( for example, 1/1, 2/1, 3/2, 8/5, 13/8, ...) the numbers produce a new sequence.
The first several terms of this new sequence are 1, 2, 1.5, 1.66..., 1.6, 1.625, 1.61538, ...
If we continue in this pattern, we will approach the decimal number 1.61803
This number can also be written as (1 + √5)/2 and it is called the golden ratio
Proof of the golden ratio
To prove that the golden ratio really approaches (1 + √5)/2, we can pull out the two 1-unit squares and the 2-unit square as shown below: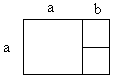
The rectangle above is called a golden rectangle. Call the side length of the 1-unit square b and the side length of the 2-unit square a
At this point, what is the golden ratio if not a pain in the neck?
In a golden rectangle, we can identify two rectangles that are similar.
A big rectangle with sides a + b and a and a small rectangle with sides b and a
If we separate the small rectangle from the bigger and rotate the big rectangle 90 degrees counterclockwise, we can easily see which sides are similar.
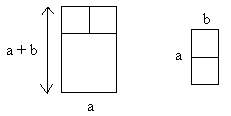
Setting up a proportion, we get: (a + b)/a = a/b
Cross multiply to get a2 = b (a + b)
a2 = ba + b2
a2 − ba − b2 = 0
Using the quadratic formula,
√(b2 − 4 × a × c)= √[(-b)2 − 4 × 1 ×(-b2)] = √(b2 + 4 b2) =√( 5 b2) = √(5)b
Therefore, a = (- -b + √(5)b)/2
a = [b + √(5)b]/2
a = b ( 1 + √(5)/2
Dividing both sides by b, we get, a/b = ( 1 + √(5))/2
Therefore, what is the golden ratio? It is not just the fascinating formula you see right above, it is also something the Pythagoreans came up with to make you spend your entire day thinking about it.
What is the golden ratio good for?
The golden ratio is especially pleasing to the eye when designing stuff.
- The Greeks used it to design a temple in Greece called Parthenon.
- The Eiffel tower was designed using the golden ratio.
- Many paintings such as Mona Lisa use the golden ratio.