Addition in base two

Addition in base two is similar to addition in base ten. Although there is a difference, it is not that hard to add in base 2

Base 10 uses 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9

The place value for base 10 is shown below:

Hundred thousands	Ten thousands	Thousands	Hundreds	tens	ones
8	7	0	4	9	7

However, a deep understanding of addition in base 10 will help you understand deeply addition in base two

Add 978 and 856 in base 10



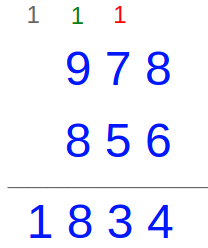
Explanation:

Add the numbers in the ones place: 8 + 6 = 14 = 10 + 4

Write 4 in the ones place and carry the 10 to the tens place. You can just use a 1 to represent the 10 (shown in red)

Add the numbers in the tens place

1 ten + 7 tens + 5 tens = 13 tens = 10 tens + 3 tens = 100 + 3 tens

Write 3 tens in the tens place and carry the 100 to the hundreds place. You can just use a 1 to represent the 100 (shown in green)

Add the numbers in the hundreds place

1 hundred + 9 hundreds + 8 hundreds = 10 hundreds + 8 hundreds = 1000 + 8 hundreds

Write 8 hundreds in the hundreds place and carry the 1000 to the thousands place. You can just use a 1 to represent the 1000 (shown in black) Bring down the 1 shown in black and you are done!


Addition in base two

We will follow the exact same pattern above to show how to add in base 2


Base 2 uses 0 and 1

We show a place value for base 2 below:

Notice that the twos place in base 2 is the tens place in base 10

Thirty-twos	Sixteens	Eights	Fours	Twos	Ones
0	1	1	0	1	0

Let's practice now with some examples


Example #1: Addition in base two with carry

To avoid confusion with base 10, we put a 2 next to each number

However, if is clear to you that the addition is being done in base 2, there is no need to write down the 2

Add: 011₂ + 101₂



Explanation:

Add the numbers in the ones place: 1 + 1 = 2 = 2 + 0.

Write 0 in the ones place and carry the 2 to the twos place. You can just use a 1 to represent the 2 (shown in red)

Add the numbers in the twos place: 1 two + 1 two + 0 two = 2 twos = 4 = 4 + 0

Write 0 in the twos place and carry the 4 to the fours place. You can just a 1 to represent the 4 (shown in green)

Add the numbers in the fours place: 1 four + 0 four + 1 four = 2 fours = 8 = 8 + 0

Put 0 in the fours place and carry the 8 to the eights place. You can just put a 1 to represent the 8 (shown in black)

Bring down the 1 shown in black et voila!



Example #2:

Add: 1101₂ + 1101₂




Explanation:

Add the numbers in the ones place: 1 + 1 = 2 = 2 + 0.

Write 0 in the ones place and carry the 2 to the twos place. You can just use a 1 to represent the 2 (shown in red)

Add the numbers in the twos place: 1 two + 0 two + 0 two = 1 two

Write 1 two in the twos place.

Add the numbers in the fours place: 1 four + 1 four = 2 fours = 8 = 8 + 0

Put 0 in the fours place and carry the 8 to the eights place. You can just put a 1 to represent the 8 (shown in green)

Add the numbers in the eights place: 1 eight + 1 eight + eight = 2 eights + 1 eight = 16 + 1 eight

Write 1 eight in the eights place and carry the 16 to the sixteens place. You can just use a 1 to represent the 16 (shown in black)

Bring down the 1 in the sixteens place shown in black et voila!

If you struggle to understand addition in base two, you may need to go back to the example I gave about base 10 and try your best to relate this to base two