Area of an equilateral triangle

The area of an equilateral triangle can be found by using the Pythagorean formula:

Start with any equilateral triangle



Label the sides.

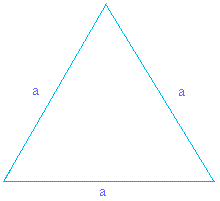
Draw the perpendicular bisector of the equilateral triangle as shown below. Note how the perpendicular bisector breaks down side a into its half or a/2



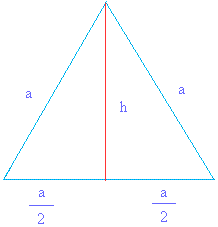
Now apply the Pythagorean theorem to get the height (h) or the length of the line you see in red


a² = (a/2)² + h²

a² = a²/4 + h²

a² − a²/4 = h²

4a²/4 − a²/4 = h²

3a²/4 = h²

h = √(3a²/4)

h = (√(3)×a)/2

Area = (base × h)/2

base × h = (a × √(3)×a)/2 = (a²× √(3))/2

Dividing by 2 is the same as multiplying the denominator by 2. Therefore, the formula is