What is the Associative Property?
The word associate in associative property may mean to join or to combine when doing addition or multiplication. It states that when adding numbers or multiplying numbers, the way that the numbers are combined using parentheses or brackets will not change the answer.
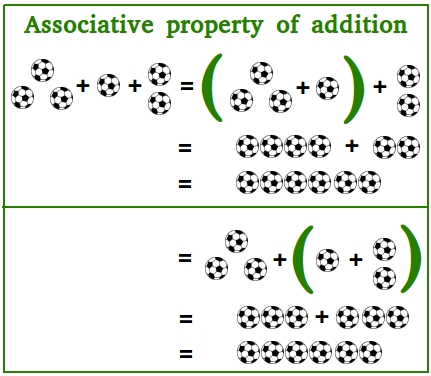
Associative property of addition
In the figure above, we are trying to perform this addition: 3 + 1 + 2
You have the choice of putting 3 and 1 together or 1 and 2 as shown below.
3 + 1 + 2 = (3 + 1) + 2
= 4 + 2
= 6
3 + 1 + 2 = 3 + (1 + 2)
= 3 + 3
= 6
Associative property of addition formula
In general for every real number A, B, and C,
A + B + C = (A + B) + C
= A + (B + C)
A real life example of the associative property
For example, suppose I go to the supermarket and buy ice cream for 12 dollars, bread for 8 dollars, and milk for 15 dollars.
How much money do I owe the cashier? The situation above is associative.
When I do my total in my head, I can combine or add the price of the ice cream and the bread first and add the result to the price of milk.
Otherwise, I can combine or add the price of bread and milk first and add the result to the price of ice cream.
Both ways of approaching the problem give the same answer.
Mathematically, you are trying to do the following: 12 + 8 + 15
You can add these three numbers in the order they appear.
12 + 8 = 20 (This is adding price of ice cream and bread first)
20 + 15 = 35
You can use parentheses to show the order in which you are adding.
(12 + 8) + 15
Another way to add is to add not according the order in which they appear.
You may decide you will add first 8 and 15
8 + 15 = 23 (This is adding price of bread and milk first)
12 + 23 = 35
Again, using parentheses to show the order in which you are adding, you get:
12 + (8 + 15)
We conclude that (12 + 8) + 15 = 12 + ( 8 + 15)
The above example illustrates the associative property of addition
Terms added in different combinations or grouping yield the same answer
Associative property of multiplication
Again, we know that the following equations are true.
(3 × 4) × 5 = 3 × (4 × 5)
(2 × 6) × 7 = 2 × (6 × 7)
(1 × 9) × 8 = 1 × (9 × 8)
All three examples given above will yield the same answer when the left-hand side and the right-hand side of the equation are multiplied.
For example, 3 × 4 = 12 and 12 × 5 = 60
Also, 4 × 5 = 20 and 3 × 20 = 60
Associative property of multiplication formula
In general for every real number X, Y, and Z,
X × Y × Z = (X × Y) × Z
= (XY)Z
X × Y × Z = X × (Y × Z)
= X(YZ)
More examples showing the associative property of multiplication
(1 × 5) × 2 = 1 × (5 × 2)
(6 × 9) × 11 = 6 × (9 × 11)
(1 + 5) + 2 = 1 + (5 + 2)
(6 + 9) + 11 = 6 + (9 + 11)
(x + 5) + 4 = x + (5 + 4)
(6 + z) + 1 = 6 + (z + 1)
(x + y) + z = x + (y + z)
(x × y) × z = x × (y × z)
Does the associative property work for division?
Warning! Although multiplication is associative, division is not associative.
Notice that (24 ÷ 6) ÷ 2 is not equal to 24 ÷ (6 ÷ 2)
(24 ÷ 6) ÷ 2 = 4 ÷ 2 = 2
However, 24 ÷ (6 ÷ 2) = 24 ÷ 3 = 8
Therefore, different combination may yield different results.
Notice that it may happen that a different grouping gives the same result.
(24 ÷ 6) ÷ 1 = 24 ÷ (6 ÷ 1)
(24 ÷ 6) ÷ 1 = 4 ÷ 1 = 4 and 24 ÷ (6 ÷ 1) = 24 ÷ 6 = 4
However, we shall not make a rule out of this because it is not true for all cases.
Finally, note that unlike the commutative property which plays around with two numbers, the associative property combines at least three numbers.
Does the associative property work for subtraction?
Try to perform the following subtraction using the associative property: 15 - 4 - 8
Is (15 - 4) - 8 equal to 15 - (4 - 8)
(15 - 4) - 8 = (11) - 8 = 3
However,
15 - (4 - 8) = 15 - (-4) = 15 + 4 = 19
Therefore, the associative property does not work for subtraction!