Distributive Property
The distributive property states that multiplying a number by an addition problem is the same as multiplying the number by each addend in the addition problem and then adding the products. If instead the number is multiplied by a subtraction problem, it is the same as the difference of the products.
Notice that the distributive property combines both multiplication and (either addition or subtraction).
Find some good examples here showing you how to use this property. Study these examples really well! As a result, you will be able to solve similar problems with ease.
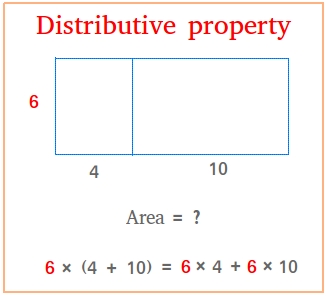
Take a look at the figure above. While trying to find the area of the rectangle, you may end up using the distributive property.
In the figure, the number that we distribute is 6 and the addends are 4 and 10. The way to distribute is to multiply 6 by 4 and 6 by 10. Finally, you can add the products if you want to get an answer.
Area = width × length
Since width = 6 and length = 4 + 10, area = 6 × (4 + 10)
6 × (4 + 10) = 6 × 4 + 6 × 10
6 × (4 + 10) = 24 + 60
6 × (4 + 10) = 84
Notice that you can also simplify 6 × (4 + 10) by following the order of operations or PEMDAS. You will do this by adding 4 and 10 and multiply what you get by 6.
6 × (4 + 10) = 6 × 14
6 × (4 + 10) = 84
Although the answer is still 84, this way of solving the problem does not show the distributive property.
Distributive property formula
6 × (4 + 10) = 6 × 4 + 6 × 10 is an example of distributive property of multiplication over addition.
In general, for every real numbers a, b, and c,
a(b + c) = ab + ac
Because of the commutative property of multiplication, you can also write the distributive property of addition as shown below.
(b + c)a = ba + ca
What happens now if you change the addition sign between 4 and 10 to a minus sign? You now have the distributive property of subtraction.
6 × (4 - 10) = 6 × 4 - 6 × 10 is a good example of distributive property of multiplication over subtraction.
In general, for every real numbers a, b, and c,
a(b - c) = ab - ac
Again, because of the commutative property of multiplication, you can also write the property as shown below.
(b - c)a = ba - ca
Is there a distributive property of division?
Yes, the distributive property can also be used in division. An example may help to illustrate this better. Divide 324 by 4.
324 / 4 = (300 + 24) / 4 = 300 / 4 + 24 / 4 = 75 + 6 = 81.
Just replace the forward slash with the division sign so you can better see the property.
(300 + 24) ÷ 4 = 300 ÷ 4 + 24 ÷ 4
The distributive property of division is mostly useful when the outer term (the number outside the parenthesis) can go evenly into each of the numbers inside the parenthesis. This will help you find the answer to a division problem quickly and avoid long division when the dividend is a larger number.
Simplify 2464 ÷ 4
Just rewrite 2464 as 2400 + 60 + 4 and then distribute the division operation in the same way you distribute the multiplication operation.
2464 ÷ 4 = (2400 + 60 + 4) ÷ 4 = 2400 ÷ 4 + 60 ÷ 4 + 4 ÷ 4 = 600 + 15 + 1 = 616
When should you use the distributive property?
1. You can use the distributive property to do multiplication quickly. For example, simplify 25(102). Instead of using the multiplication algorithm, which can take a long time, you can use the distributive property to quickly get an answer.
25(102) = 25(100 + 2) = 25(100) + 25(2) = 2500 + 50 = 2550
In the previous section, did you notice how we used the distributive property of division to quickly divide 2464 ÷ 4?
2. You can also use the distributive property when the inner terms or the terms inside the parentheses are not like terms. This can happen for instance if you have a combination of different variables and numbers inside the parenthesis.
For example, multiply 4 by (x + 5).
Since x and 5 are not like terms, you cannot add x and 5. The logical and natural thing to do is to use the distributive property to simplify this expression.
4(x + 5) = 4(x) + 4(5) = 4x + 20
A couple of distributive property examples in the real-world
Example #1:
You go to the supermarket to buy some items that you need. One bag of apples costs 3 dollars and one gallon of olive oil costs 15 dollars. If you get 4 bags of apples
and 4 gallons of olive oil, how much money do you pay the cashier?

Total cost = 4 × (3 + 15) = 4 × 3 + 4 × 15
Total cost = 4 × (3 + 15) = 12 + 60
Total cost = 4 × (3 + 15) = 72
Example #2:
Robert has 8 notebooks and his brother has 6 notebooks. If we double both amount, how many do they now have altogether?
This word problem can be written as 2 × ( 8 + 6)
2 × ( 8 + 6) = 2 × 8 + 2 × 6
2 × ( 8 + 6) = 16 + 12
2 × ( 8 + 6) = 28
Notice again that we get the same answer if we add 8 and 6 and multiply the result by 2. However, this way of solving the problem will not show the distributive property.
Similarity and difference between the distributive property and FOIL
The FOIL method is actually derived from the distributive property but FOIL is only used to find the product of two binomials, such as multiplying (x + 1) by (x + 3).
The distributive property can be used though to solve problems that are more complex than the multiplication of two binomials.
For example, suppose you want to multiply a binomial by a trinomial, the distributive property can come very handy in helping you breaking down the problem in smaller manageable pieces.
Multiply (x + 2) by (2x + y + 2).
You can just let a = x + 2 and use the distributive property.
(x + 2)(2x + y + 2) = a(2x + y + 2) = 2xa + ay + 2a
Replace a by its value
2xa + ay + a = 2x(x + 2) + (x + 2)y + 2(x + 2)
Use the distributive property again.
2xa + ay + a = 2x2 + 4x + xy + 2y + 2x + 4
Add like terms
2xa + ay + a = 2x2 + 6x + xy + 2y + 4