Central angles

This lesson offers a concise, but thorough explanation of central angles, but also of arcs and sectors of a circle.

Definition: An angle is a central angle if it meets the following two conditions

1) The vertex of the angle is located at the center of a circle.

2) The rays that make up its sides are radii of the circle. Below, find an illustration of the definition above:


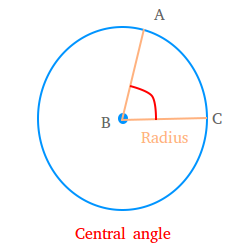
You can name it angle ABC.It is important to notice that such angle is always less than 180 degrees.

Therefore, such angles can only be acute or obtuse

Related definitions:

Arc:

A portion of the circumference of the circle. This is illustrated below in red:



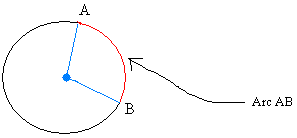
Sector:

A sector is the area enclosed within a central angle and an arc. Again, this is illustrated below, but in green:



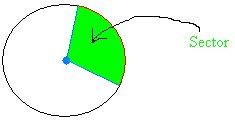
As you can see, the area in green is included between the arc in red and the angle

When computing the area of a sector, use the following ratio or formula to find out what part of the circle's area is covered by the sector:

A computation!

A circle has a radius of 10 centimeters. This radius and the center of the circle is used to make of angle of 45 degrees. Find the area of the resulting sector

Divide 45 degrees divided by 360 degrees to determine the fraction of the circle covered by this sector 45/360 = 1/8

The area of the circle is

A = pi × r²

A = 3.14 × 10²

A = 3.14 × 10 × 10

A = 3.14 × 10²

A = 3.14 × 100

A = 314 square centimeters

Now just mutliply 314 by 1/8

314 × 1/8 = 314/8 = 39.25

The area of the sector is 39.25 square centimeters

Here we go.If you have any questions about this lesson, do not hesitate to contact me.

Now try to do this problem on your own.

A circle has a radius of 5 centimeters. This radius and the center of the circle is used to make of angle of 60 degrees. Find the area of the resulting sector