Types of Angles
Learning Angle Types with an Interactive Lesson and Quiz
There are many different types of angles and these can be classified based on the following characteristics.
- Magnitude of the angle
- Rotation of the angle
- A pair of angles
- Angles formed when a transversal cuts two parallel lines
First, let us see what an angle is and then we will show all the different types of angles .
What are angles?
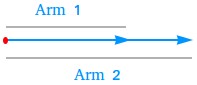
Notice that an angle is formed when two rays, also called arms of the angle, meet at a common endpoint called vertex of the angle.
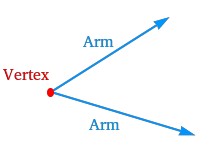
In the figure above, the vertex is shown with a red dot and the arms are shown in blue.
Classification of angles based on their magnitude
We will define the basic angles. Here is a list of 7 types of angles based on the magnitude of the angle.
- Acute angle
- Right angle
- Obtuse angle
- Straight angle
- Reflex angle
- Full rotation angle
- Zero angle
Study the images carefully so you understand them and then be able to recognize these basic angles quickly.
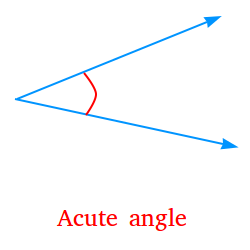
Acute angle:
An angle whose measure is less than 90 degrees is an acute angle. For example, if the magnitude of an angle is 89 degrees, the angle is acute. The angle below is an acute angle.
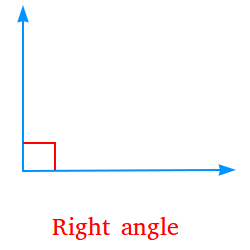
Right angle:
An angle whose measure is exactly 90 degrees. The following is a right angle.
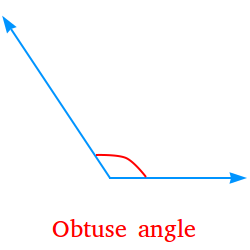
Obtuse angle:
An angle whose measure is bigger than 90 degrees but less than 180 degrees is an obtuse angle. Thus, it is between 90 degrees and 180 degrees. For example, if the measure of an angle is 150 degrees, the angle is obtuse. The following is an obtuse angle.
Straight angle:
An angle whose measure is exactly 180 degrees. Thus, a straight angle looks like a straight line. The following is a straight angle.
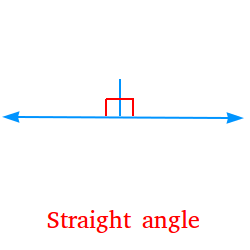
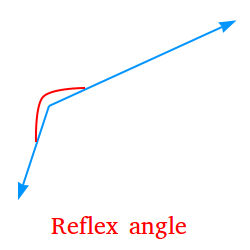
Reflex angle:
An angle whose measure is bigger than 180 degrees but less than 360 degrees. For example, if the measure of an angle is 235 degrees, the angle is a reflex angle. The following is a reflex angle.
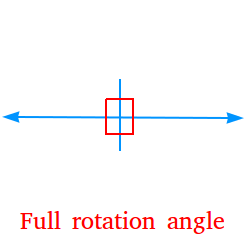
Full rotation angle:
An angle whose measure is exactly 360 degrees is a full rotation angle. A full rotation angle consists of 4 right angles. The following is a full rotation angle.
Zero angle:
An angle whose measure is exactly 0 degree is a zero angle. A zero degree angle has both arms on the same line. The following is a zero degree angle.
Classification of angles based on the rotation of the angle
Two types of angles are formed when the angle is either measured in counterclockwise direction, or a clockwise direction.
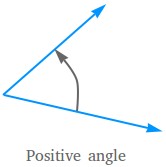
If we measure an angle counterclockwise or in the opposite direction the hands of a clock move, the angle is a positive angle. The angle below is a positive angle.
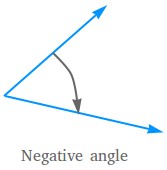
If we measure an angle clockwise or in the same direction the hands of a clock move, the angle is a negative angle. The angle below is a negative angle.
Types of angles based on a pair of angles
Here is a list of 4 types of angles based on a pair of angles.
- Adjacent angles
- Complementary angles
- Supplementary angles
- Vertical angles
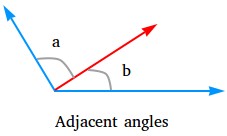
Adjacent angles:
Angles with a common vertex and one common side are called adjacent angles.
<a and <b are adjacent angles and the common side is red.
Complementary angles:
Two angles whose measures add to 90 degrees are complementary angles. Angle x and angle y shown below are complementary angles because together they form a right angle.
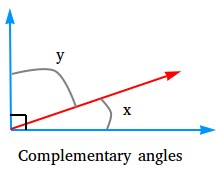
For example, suppose angle x is equal to 30 degrees and angle y is equal to 60 degrees. Since 30 degrees + 60 degrees = 90 degrees, angle x is the complement of angle y (another way to say they are complementary).
Note that angle 1 and angle 2 do not have to be adjacent to be complementary as long as they add up to 90 degrees.
Supplementary angles:
Two angles whose measures add to 180 degrees are supplementary angles. Angle c and angle d shown below are supplementary angles because together they form a straight angle.
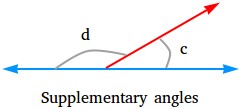
For example, suppose angle c is equal to 70 degrees and angle d is equal to 110 degrees. Since 70 degrees + 110 degrees = 180 degrees, angle c is the supplement of angle d (another way to say they are supplementary).
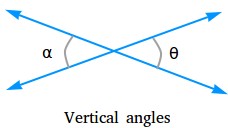
Vertical angles:
Angles that have a common vertex and whose sides are formed by the same lines are called vertical angles or opposite angles. Angle α (alpha) and angle θ (theta) are vertical angles.
Types of angles can be based on the angles formed when a transversal cuts two parallel lines
When two parallel lines are crossed by a third line (Transversal), 8 angles are formed. Take a look at the following figure.
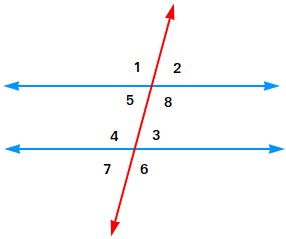
Angles 3,4,5,8 are interior angles
Angles 1,2,6,7 are exterior angles
Alternate interior angles:
Alternate interior angles are pairs of interior angles on opposite sides of the transversal.
For instance, angle 3 and angle 5 are alternate interior angles. Angle 4 and angle 8 are also alternate interior angles.
Alternate exterior angles:
Alternate exterior angles are pairs of exterior angles on opposite sides of the transversal.
Angle 2 and angle 7 are alternate exterior angles.
Corresponding angles:
Pairs of angles that are in similar positions are corresponding angles
Angle 3 and angle 2 are corresponding angles.
Angle 5 and angle 7 are corresponding angles
Here we go! Study the types of angles carefully. This is where any serious study of geometry begin.