Complementary and Supplementary Angles
Before we provide you with a definition of complementary and supplementary angles, here is an important reminder about adjacent angles.
Adjacent angles: Adjacent angles are angles that share a vertex and a common side. This fact is important to keep in mind because many complementary and supplementary angles that you will be dealing with in geometry are adjacent angles.
Complementary angles:
Two angles whose measures add to 90 degrees. It is easy to see when the angles are adjacent like the following:
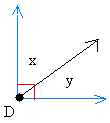
Angle x and angle y are adjacent angles because they share a ray (line in black) and a vertex (point in black called D).
Now why are angle x and angle y complementary? Notice also that the angle in blue measures 90 degrees.
Since the measure of angle x plus the measure of angle y = 90 degrees, x and y are complementary.
Each angle is called the complement of the other. For example, you could also say that angle x is the complement of angle y.
Angles do not have to be adjacent to be complementary. The following angles are also complementary. As long as the sum of the measures equal 90 degrees, the angles are complementary.

Supplementary angles:
Two angles whose measures add to 180 degrees. It is easy too to see this when the angles are adjacent like the following:
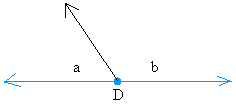
Again, angle a and angle b are adjacent angles because they share a ray (line in black) and a vertex (point in black called D).
Now why are they supplementary?
Notice also that the angle in blue measures 180 degrees because the angle is a straight line and a straight line measures 180 degrees.
Since the measure of angle a plus the measure of angle b = 180 degrees, a and b are supplementary angles
Each angle is called the supplement of the other. For example, you could also say that angle a is the complement of angle b.
Again, angles do not have to be adjacent to be supplementary. The following angles are also supplementary since the sum of the measures equal 180 degrees

Can three or more angles be complementary or supplementary? No way!
The definition of complementary and supplementary angles apply only to two angles. Therefore, even if 3 angles or more add up to 90 or 180 degrees, we do not call them complementary or supplementary angles.