Counting factors
Counting factors is really useful when you are looking for the factors of a number. You may need this information if you do not want to miss any factors.
To count factors, first we need to get the prime factorization of the number.
Example #1:
How many factors does 8 have?
The factors of 8 are 1, 2, 4, 8, so there are 4 factors.
Looking at 23, we notice that if we add 1 to the exponent, we get the 4.
However, just one case is not enough to conclude that when counting factors the number of factors is whatever the exponent is plus 1.
Let's look at more examples
Example #2:
How many factors does 25 have?
25 = 5 × 5 = 52.
The factors of 25 are 1, 5, and 25, so 25 has 3 factors.
Again, to get the 3, just add 1 to the exponent of 2.
Example #3:
How many factors does 72 have?
72 = 8 × 9 = 2 × 2 × 2 × 3 × 3 = 23 × 32.
The factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72, so there are 12 factors.
How do we get the 12? By adding 1 to each exponent and then multiply
(3 + 1) × (2 + 1) = 4 × 3 = 12
So far it seems like adding 1 is a good strategy when counting factors.
Another way to see all the factors of 72 are shown below:
20 × 30 = 1 × 1 = 1
20 × 31 = 1 × 3 = 3
20 × 32 = 1 × 9 = 9
21 × 30 = 2 × 1 = 2
21 × 31 = 2 × 3 = 6
21 × 32 = 2 × 9 = 18
22 × 30 = 4 × 1 = 4
22 × 31 = 4 × 3 = 12
22 × 32 = 4 × 9 = 36
23 × 30 = 8 × 1 = 8
23 × 31 = 8 × 3 = 24
23 × 32 = 8 × 9 = 72
As you can see there are 4 choices for the exponents of 2: 0, 1, 2, 3.
And 3 choices for the exponents of 3: 0, 1, 2.
4 choices × 3 choices = 12 choices and this is equal to 12 factors
Example #4:
How many factors 12600 have?
When counting factors for big numbers, it may be useful to make a factor tree.
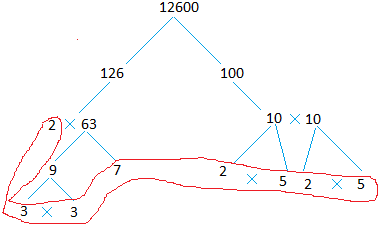
Pull out all the prime numbers from the tree and multiply the numbers. This is your prime factorization.
2 × 2 × 2 × 3 × 3 × 5 × 5 × 7
23 × 32 × 52 × 71
Add 1 to each exponent and multiply:
(3 + 1) × (2 + 1) × (2 + 1) × (1 + 1)
4 × 3 × 3 × 2
12 × 3 × 2
36 × 2 = 72
12600 has 72 factors.

