Basic Mathematics Blog
The Basic Mathematics Blog will let you know when a new topic or lesson is added to my website. Keep scrolling down to see all of our latest math lessons.
Dec 17, 2024
Common Mistakes in Math
Some common mistakes in math and how to avoid them when doing your math problems
Dec 13, 2024
Solving Proportions - Interactive Lesson
Solving proportions by using cross product or the concept of equivalent fractions
Dec 09, 2024
Perfect Number
Discover perfect numbers through clear definitions, examples, the first ten, historical significance, and their relationship with Mersenne primes in this lesson.
Dec 08, 2024
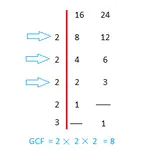
Greatest Common Factor
Interactive lesson showing three methods to find the the greatest common factor of two whole numbers.
Dec 06, 2024
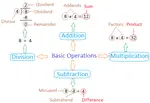
Basic Number Properties
Learn about the 4 basic number properties such as such as commutative, associative, distributive, and identity properties.
Dec 06, 2024
Percentage Change
Master percentage change calculations with clear step-by-step methods, examples, and tips. Learn to handle increases, decreases, and negative values.
Dec 05, 2024
Factoring by Grouping with an Interactive Lesson
Learn factoring by grouping with interactive lesson, step-by-step guidance, instant feedback, and clear solutions to help you master factoring effortlessly.
Continue reading "Factoring by Grouping with an Interactive Lesson"
Dec 04, 2024
Estimating a Sum
Estimating a sum by rounding to the nearest 10 or to the nearest 100 and choosing the best estimate
Nov 26, 2024
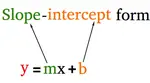
Slope Intercept Form
Interactive lesson and practice showing how to use the slope and one or two points to write the equation of line in slope intercept form.
Nov 21, 2024
What is Slope? Definition, Exploration, and Examples
What is slope? Definition of slope, interactive exploration, along with concrete examples to enhance understanding.
Continue reading "What is Slope? Definition, Exploration, and Examples"
Nov 20, 2024
Terminating Decimals to Fractions
Learn how to convert terminating decimals to fractions with an interactive and animated lesson
Nov 20, 2024
Decimal Place Value
To identify and get an understanding of decimal place value with an interactive lesson and quiz
Nov 11, 2024
What are Exponents ? Definition, Examples, and Quiz
An interactive lesson and quiz on exponents with interactive questions, helping you learn through both input and click-based exercises
Continue reading "What are Exponents ? Definition, Examples, and Quiz"
Nov 08, 2024
Basic Mathematics Games
A variety of basic mathematics games that will really help you sharpen your basic mathematics skills with unlimited practices.
Nov 07, 2024
Divisibility Rules Game
A very interactive divisibility rules game that will really help you sharpen your basic mathematics skills while you play against an opponent
Nov 07, 2024
Comparing Integers Game
A very interactive comparing integers game that will really help you sharpen your basic mathematics skills.
Nov 05, 2024
Arithmetic Game with Number Ninja
Practice adding, subtracting, and multiplying and dividing with number ninja, a fun and interactive arithmetic game
Nov 04, 2024
Prime Number Game - May the Hunt Begin!
An interactive prime number game that will engage students every step of the way and sharpen their basic mathematics skills.
Oct 31, 2024
Factoring Trinomials of the Form x^2 + bx + c | Interactive Lesson
Factoring trinomials (ax^2 + bx + c ) when a = 1 with an interactive lesson. See how how quick you can learn how to factor with step-by-step prompt
Continue reading "Factoring Trinomials of the Form x^2 + bx + c | Interactive Lesson "
Oct 30, 2024
Fractions - Interactive Lesson and Quiz Mode
Introduction to fractions using pizzas as a real-world example and an interactive lesson.
Continue reading "Fractions - Interactive Lesson and Quiz Mode"
Oct 27, 2024
Cartesian Coordinate System
Interactive lesson about the Cartesian coordinate system and how it is used to locate points
Oct 22, 2024
Basic Math Calculator
Use these basic math calculator to strenghten your basic math skills.
Oct 21, 2024
Unlimited Area of Triangles Worksheet
Look for the area of triangles by generating unlimited worksheets using a visual format and a text-based format
Oct 20, 2024
Unlimited Pythagorean Theorem Worksheet with answers
This Pythagorean theorem worksheet will help students clearly understand the Pythagorean theorem while allowing teachers to print unlimited worksheets
Continue reading "Unlimited Pythagorean Theorem Worksheet with answers"
Oct 18, 2024
Subtracting Whole Numbers
Subtracting whole numbers vertically by regrouping ( also called borrowing ) is what this lesson will teach you
Oct 18, 2024
Basic Math Formulas
A comprehensive list of the most commonly used basic math formulas. If you are looking for a formula to solve your math problems, your formula is likely here
Oct 10, 2024
Root Calculator(√)
Find the root of any number such as the square root, cube root, along with step-by-step explanations
Oct 09, 2024
Adding and Subtracting Polynomials Calculator
Add and subtract polynomials with this calculator. See step-by-step how the answer was found
Continue reading "Adding and Subtracting Polynomials Calculator"
Oct 08, 2024
Factors Calculator - Step-by-Step
Use this factors calculator to display all factors of a number and see step-by-step explanations
Oct 08, 2024
Online Age Calculator - How Old are You?
How old are you? This online age calculator to find your age to the nearest second.
Oct 07, 2024
Percentage Calculator - Step-by-Step
Use this percentage calculator to find the percentage(is in "x% of is"), the rate(x%) or the base(number after of) step-by-step
Oct 07, 2024
Percentage Change Calculator
The percentage change calculator will compute the percentage increase/decrease and show you step-by-step solution
Oct 07, 2024
Average Calculator
The average calculator will display the average along with step-by-step explanation for an infinite amount of numbers
Oct 04, 2024
Decimal to Fraction Calculator
This decimal to fraction calculator will convert any decimal to a fraction. Step-by-step solution is included!
Oct 04, 2024
Cube Calculator - Step-by-Step Solutions
The cube calculator will find all values (step-by-step) when either the side length, volume, surface area, face diagonal, or solid diagonal is given
Oct 02, 2024
Slope Calculator
Use this slope calculator to see step-by-step how to find the slope of a line and the forms of an equation
Oct 02, 2024
Pythagorean Theorem Calculator
Use this Pythagorean theorem calculator to find the hypotenuse or one of the legs of a right triangle
Oct 02, 2024
Circle Calculator
The circle calculator will find 3 values when either the area, the circumference, the radius, or the diameter is given
Oct 01, 2024
Least common multiple calculator
This easy to use least common multiple calculator will help you find the smallest multiple two numbers have in common.
Oct 01, 2024
Greatest Common Factor Calculator
Use this easy to use greatest common factor calculator to find the highest factor two numbers have in common.
Sep 29, 2024
Math Millionaire - Review Basic Math skills
Math millionaire will help you review basic math skills in a fun and engaging way
Continue reading "Math Millionaire - Review Basic Math skills"
Sep 26, 2024
Fractions Calculator
This fractions calculator will help you add, subtract, multiply, and divide an unlimited number of fractions from the simplest to the most complex expression
Sep 25, 2024
Add and Subtract Integers Calculator
add and subtract unlimited integers step-by-step with this calculator
Sep 23, 2024
Adding and Subtracting Fractions Step by Step
Use this adding fractions calculator to add or subtract an unlimited number of fractions step by step.
Continue reading "Adding and Subtracting Fractions Step by Step"