Factoring trinomials is the inverse of multiplying two binomials. Instead of multiplying two binomials to get a trinomial, you will write the trinomial as a product of two binomials.
Equation:
Find factor pairs that multiply to c =
Calculate the sum of each factor pair found:
| Factor Pair | Sum |
|---|
Which factor pair sums to b = ?
Express the quadratic in its factored form:
The general form of a trinomial is ax2 + bx + c. Your goal when factoring trinomials is to make ax2 + bx + c equal to (? + ?) × (? + ?).
When a = 1, the trinomial becomes x2 + bx + c and it is easier to factor. This lesson will only show you how to factor when a = 1.
Example #1:
Factor x2 + 5x + 6
x2 + 5x + 6 will look like (x + ?) × (x + ?)
Be 100% sure that the first term for each binomial must be x because x × x = x2.
Now, how do we get the second term for each binomial? We also know for sure that ? × ? or the product of the second term for each binomial is equal to 6.
Finally, we know that x × ? and ? × x must give the second term, which is 5x when added.
x × ? + ? × x = x (? + ?)
So the two numbers we do not know must also be added as shown with ? + ?.
They must be multiplied to get 6 and at the same time they must be added to get 5. The two numbers that will work are 2 and 3 since 2 times 3 is equal to 6 and 2 plus 3 is equal to 5.
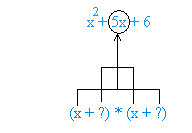
Thus, when factoring trinomials, the trick is to look for factors of the last term that will add up to the coefficient of second term.
The last term of x2 + 5x + 6 is 6 and the coefficient of the second term is 5. Sometimes it may be useful to list all the factor pairs as shown below.
6 is equal to:
6 × 1
-6 × - 1
2 × 3
-2 × -3
Again, the only pair of factors that will add up to 5 is 2 and 3 because 2 + 3 = 5. Just replace the two question mark by 2 and 3 and you are done.
Therefore, x2 + 5x + 6 = (x + 3) × (x + 2)
Notice that (x + 3) × (x + 2) is also equal to (x + 2) × (x + 3) since multiplication is commutative.
The final step is to check your answer by multiplying the two binomials.
x × x = x2
x × 2 = 2x
3 × x = 3x
3 × 2 = 6
Since 2x + 3x = 5x, putting it all together, we get x2 + 5x + 6
Example #2:
Factor x2 − 5x + 6
It is almost the same equation as before with the exception that the coefficient of the second term is -5 instead of 5.
Follow all steps outlined above. The only difference is that you will be looking for factors of 6 that will add up to -5 instead of 5.
Since -3 and -2 will do the job, x2 − 5x + 6 = (x + -3) × (x + -2)
Final example
Factor x2 − x − 20
First, notice that x2 − x − 20 = x2 − 1x − 20 because 1 × x = x
x2 − x − 20 = (x + ?) × (x + ?)
Find factors of -20 that will equal to -1
-20 is equal to
-20 × 1
20 × -1
10 × -2
-10 × 2
4 × -5
-4 × 5
Since 4 + -5 = -1, we have found what we need.
x2 − x − 20 = (x + 4) × (x + -5)