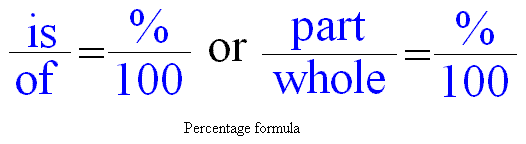Formula for Percentage

The formula for percentage is the following and it should be easy to use if you follow the straightforward directions given. Study the formula below carefully before looking at the examples.

Formula for percentage

We will take some examples to illustrate. Let us start with the formula on the left.

An important thing to remember is to cross-multiply after you have identified the different parts of the formula.

Cross-multiply means to multiply the numerator of one fraction by the denominator of the other fraction.

How to Use the Formula for Percentage on the Left

Example #1:

25 % of 200 is ____

In this problem, of = 200, is = ?, and % = 25

We get:

is/200 = 25/100

Since is in an unknown, you can replace it by y to make the problem more familiar.

y/200 = 25/100

Cross multiply to get y × 100 = 200 × 25

y × 100 = 5000

Divide 5000 by 100 to get y

Since 5000/100 = 50, y = 50

So, 25 % of 200 is 50


Example #2:

What number is 2% of 50 ?

This is just another way of saying 2% of 50 is ___

So, set up the proportion as example #1:

is/50 = 2/100

Replace is by y and cross multiply to get:

y × 100 = 50 × 2

y × 100 = 100

Since 1 × 100 = 100, y = 1

Therefore, 1 is 2 % of 50


Example #3:

24% of ___ is 36

This time, notice that is = 36, but of is missing

After you set up the formula, you get:

36/of = 24/100

Replace of by y and cross multiply to get:

36/y = 24/100

y × 24 = 36 × 100

y × 24 = 3600

Divide 3600 by 24 to get y

3600/24 = 150, y = 150

Therefore, 24 % of 150 is 36

How to Use the Other Formula for Percentage on the Right

Now, we will take examples to illustrate how to use the formula for percentage on the right

Example #4:

To use the other formula that says part and whole, just remember the following:

  • The number after of is always the whole.
  • The number after is is always the part.
If a problem says 25 % of ___ is 60, then, we know that the whole is missing and the part = 60

Your proportion will like this:

60/whole = 25/100

After cross multiplying, we get:

whole × 25 = 60 × 100

whole × 25 = 6000

Divide 6000 by 25 to get whole

6000/25 = 240, so whole = 240

Therefore, 25 % of 240 is 60


Example #5:

___% of 45 is 9

Here whole = 45 and part = 9, but % is missing

We get:

9/45 = %/100

Replacing % by x and cross multiplying gives:

9 × 100 = 45 × x

900 = 45 × x

Divide 900 by 45 to get x

900/45 = 20, so x = 20

Here we go! I hope the formula for percentage was helpful.

Finding a percentage