How to Find the Slope

Here is how to find the slope. We saw in the lesson about what is slope that slope is a measure of how steep a line is and the steepness of the line can be measured with the following formula: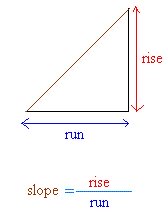

How to find the slope when the rise and the run are known

Let's illustrate this with some examples: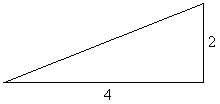


For this situation, we see that the rise is 2 and the run is 4, so slope = 2/4

slope = 1/2 after simplification.

what is the meaning of 1/2 ?

Since 1/2 is positive, you are going uphill. Now, suppose the unit is yard.

1 is the rise and 2 is the run. This means that every time you go up 1 yard, you go across or horizontally 2 yards.

This situation is not very steep. However, take a look at the following:


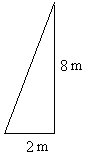
Here, the rise is 8 and the run or horizontal distance is 2

So, slope = 8/2 = 4 meters.

4 meters = 4/1 meters. This means that each time you go 4 meters straight up, you only go 1 meter horizontally.

This situation is very steep because you go up a lot more compared to going horizontally.

How to find the slope when we don't know the rise and the run.

If we graph the slope on the coordinate system, we will be able to derive another useful formula.

Let us then try to put a slope of 4 as in the previous example on the coordinate system.

Put a rise of 8 anywhere you wish. Then, put a run of 2. Here we go!

Draw the slope (in red)

If we remove everything in blue(rise and run), you are left with just the slope of the line.

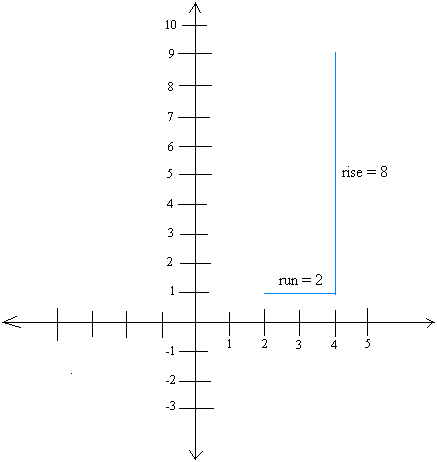
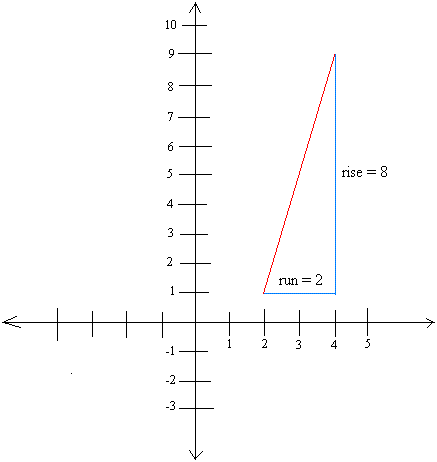
Then, label the two endpoints with their respective coordinates.

The two coordinates (4, 9) and (2,1) can be used to get a slope of 4.

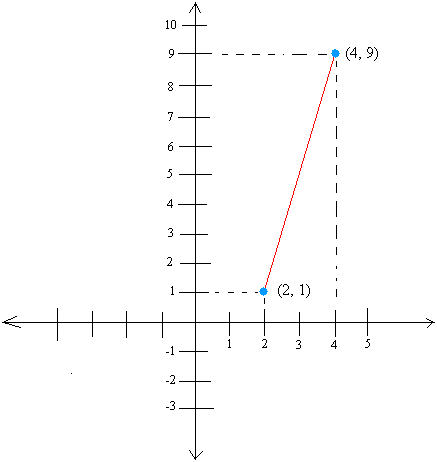
Notice that 9 − 1 = 8 and 9 and 1 represent y-coordinates.

Since we cannot call both coordinates y, we can call one y₁ and call the other y₂

Let y₁ = 9

Let y₂ = 1

Therefore, 9 − 1 = y₁ − y₂ = 8 = rise

Notice also by the same token that 4 − 2 = 2 and 4 and 2 represent x-coordinates.

Since we cannot call both coordinates x, we can call one x₁ and call the other x₂

Let x₁ = 4

Let x₂ = 2

Therefore, 4 − 2 = x₁ − x₂ = 2 = run

We can see then that

y₁ − y₂ = rise and

x₁ − x₂ = run

The formula becomes:

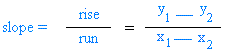
So, if the rise and the run are not given, but you know at least two points, use the formula right above.

Examples: How to find the slope when points are given.

1) (8, 8) and (4, 4)

Let (x₁,y₁) = (8, 8) and (x₂,y₂) = (4, 4)

(y₁ − y₂) / (x₁ − x₂) = (8 − 4 )/(8 − 4 ) = 4/4 = 1

Since 1 is positive, the line goes up as you move from left to right

2) (1, -5) and (2, -10)

Let (x₁,y₁) = (1, -5) and (x₂,y₂) = (2, -10)

(y₁ − y₂) / (x₁ − x₂) = (-5 − -10 )/(1 − 2) = (-5 + + 10)/-1 = 5/-1 = -5

Since -5 is negative, the line goes down as you move from left to right

Notice that

(y₂ − y₁) / (x₂ − x₁)= (-10 − -5 )/(2 − 1) = (-10 + + 5)/1 = -5/1 = -5

In general slope = (y₁ − y₂) / (x₁ − x₂) = (y₂ − y₁) / (x₂ − x₁)

Now don't you wonder anymore about how to find the slope!

How to find the slope quiz. Find out how well you understand this lesson.