Mayan numeration system

The Mayan numeration system evolved around A.D. 300. It is a sophisticated system as you will see below.

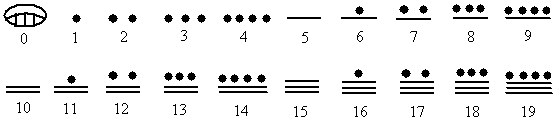
It uses 3 basic numerals to represent any possible number: a dot for one, a horizontal bar for 5, and a conch shell for zero.


They used the 3 symbols above to represent the numbers from 0 through 19 as shown below:

Numbers bigger than 19 in the Mayan numeration system

For number bigger than 19, a number is written in a vertical position so that it becomes a vertical place value system.

Initially, the base used in the Mayan numeration system was base 20 and their place values were 1, 20, 20²,20³, ...

Then, they changed their place values to 1, 20, 20 × 18, 20² × 18, 20³× 18, ...

Using the base 20, 1, 20, 20²,20³, ..., we can write 20 as follow:


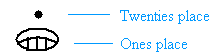
In the ones place we have 0 and in the twenties place we have 1, so the number is 0 × 1 + 1 × 20 = 0 + 20 = 20

Still using a base of 20, we can write 100 as follow:


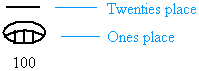
0 × 1 + 5 × 20 = 0 + 20 = 100

Here is how to represent 2007


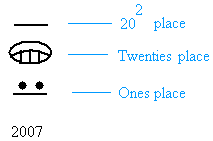
5 × 20² + 0 × 20 + 7 = 5 × 400 + 0 + 7 = 2000 + 7 = 2007

How do we know which number is in what place value?. This is the complicated part in the Mayan numeration system.

Starting from the bottom, a place value must have a number from the list above (1-19)

Tease your brain with the following number. What is it?


Look carefully and see how I separated the place values.


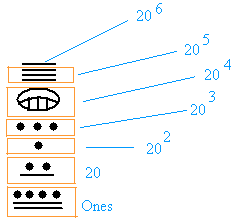
Again, I separated according to numbers that are the list above from 1 through 19.

The number is: 14 + 7 × 20 + 1 × 20² + 3 × 20³ + 0 × 20⁴ + 15 × 20⁵ + 5 × 20⁶

The number is 14 + 140 + 1 × 400 + 3 × 8,000 + 0 + 15 × 3,200,000 + 5 × 64,000,000

The number is = 14 + 140 + 400 + 24,000 + 0 + 48,000,000 + 320,000,000 = 368024554

With the base 1, 20, 20 × 18, 20² × 18, 20³× 18, ... computation is done the exact same way!


Group as shown below:

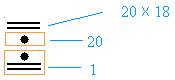
The number is 11 × 1 + 1 × 20 + 10 × 20 × 18 = 11 + 20 + 3600 = 3631

No doubt, the Mayan numeration system was sophisticated.