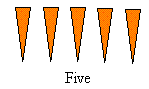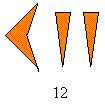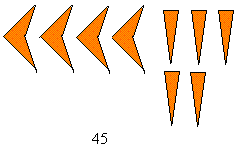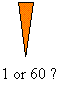Babylonian numeration system

The Babylonian numeration system was developed between 3000 and 2000 BCE.
It uses only two numerals or symbols, a one and a ten to represent numbers and they looked this these

To represent numbers from 2 to 59, the system was simply additive

Example #1:

5 is written as shown:

12 is written as shown:

Notice how the ones, in this case two ones are shown on the right just like the Hindu-Arabic numeration system

45 is written as shown:

For number bigger than 59, the Babylonian used a place value system with a base of 60

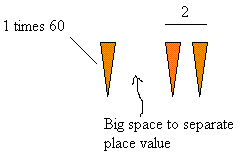
62 is written as shown:

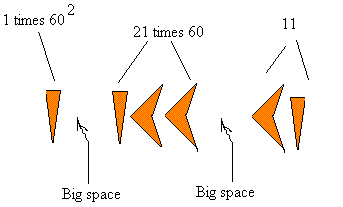
Notice this time the use of a big space to separate the space value

Without the big space, things look like this:

However, what is that number without this big space? Could it be 2 × 60 + 1 or 1× 60² + 1 × 60 + 1 or .....???


The Babylonians introduced the big space after they became aware of this ambiguity.

The number 4871 could be represented as follow: 3600 + 1260 + 11 = 4871


Even after the big space was introduced to separate place value, the Babylonians still faced a more serious problem?

How would they represent the number 60?

Since there was no zero to put in an empty position, the number 60 would thus have the same representation as the number 1

How did they make the difference? All we can say is that the context must have helped them to establish such difference yet the Babylonian numeration system was without a doubt a very ambiguous numeral system



If this had become a major problem, no doubt the Babylonians were smart enough to come up with a working system