Mixture word problems
There are many examples of mixture word problems. The goal is to really help you understand deeply a few of these word problems .Then, you will be able to tackle similar problems on your own.Example #1:
A store owner wants to mix cashews and almonds. Cashews cost 2 dollars per pound and almonds cost 5 dollars per pound. He plans to sell 150 pounds of a mixture. How many pounds of each type of nuts should be mixed if the mixture will cost 3 dollars?
Solution #1: Use of one variable leading to a linear equation
Let x be the number of pounds of cashews.
So, 150 - x will represent the number of almonds.
Since each pound of the mixture costs 3 dollars, 150 pounds will cost 3 × 150 = 450 dollars.
Cost of cashews + cost of almonds = 450
2 × x + (150 - x) × 5 = 450
2x + 150 × 5 - x × 5 = 450
2x + 750 - 5x = 450
2x - 5x + 750 = 450
-3x + 750 = 450
-3x + 750 - 750 = 450 - 750
-3x = -300
-3x/-3 = -300/-3
x = 100
150 - x = 150 - 100 = 50.
The store owner should mix 100 pounds of cashews with 50 pounds of almonds.
Solution #2: Use of two variables leading to a system of linear equations.
Let x represent the number of pounds of cashews.
Let y be the number of pounds of almonds.
x + y = 150
2x + 5y = 450
Solve by elimination
Multiply x + y = 150 by -2
-2(x + y) = 150 × -2
-2x + -2y = -300
Put the two equations together again.
-2x + -2y = -300
2x + 5y = 450
Add the left sides and the right sides to get:
3y = 150
3y/3 = 150/3
y = 50
More mixture word problems
Example 2 and 3 are more challenging mixture word problems.
Example #2
Suppose a car can run on ethanol and gas and you have a 15 gallons tank to fill. You can buy fuel that is either 30 percent ethanol or 80 percent ethanol.
How much of each type of fuel should you mix so that the mixture is 40 percent ethanol?
Solution #1: Use of one variable leading to a linear equation
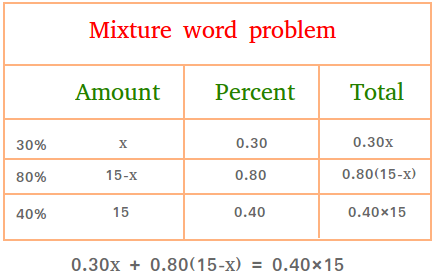
Let 15 - x be number of gallons of gas that contain 80 percent ethanol.
Since the mixture contains 40 percent ethanol, only 40% of the 15 gallons will be ethanol.
40% of 15 = (40/100) times 15 = (40/100) times 15/1 = (40 × 15) / (100 × 1) = 600 / 100 = 6
In order for x gallons of gas to contain 30% ethanol, we must take 30% of x or 30% times x
In order for 15 - x gallons of gas to contain 80% ethanol, we must take 80% of 15 - x or 80% times 15 - x
0.30 × x + 0.80 × (15 - x) = 6
0.30x + 0.80 × 15 - 0.80 × x = 6
0.30x + 12 - 0.80x = 6
0.30x - 0.80x + 12 = 6
-0.50x + 12 = 6
-0.50x = -6
x = 12
So 12 gallons of gas contain 30 percent ethanol and 15 - 12 = 3 gallons contain 80 percent ethanol.
Therefore, mix 12 gallons of a 30% ethanol with 3 gallons of an 80% ethanol.
Indeed 30% of 12 = 0.30 × 12= 3.6 and 80% of 3 = 0.80 × 3 = 2.4
3.6 + 2.4 = 6
Solution #2: Use of two variables leading to a system of linear equations.
Le x be number of gallons of gas that contain 30 percent ethanol.
Let y represent number of gallons of gas that contain 80 percent ethanol.
x + y = 15
0.30 × x + 0.80 × y = 0.40 × 15
x + y = 15
0.30x + 0.80y = 6
Solve by substitution
Use x + y = 15 to get x (subtract y from both sides) and replace x into the other equation
x = 15 - y
0.30 × (15 - y) + 0.80y = 6
0.30 × 15 - 0.30 × y + 0.80y = 6
4.5 + 0.80y - 0.30y = 6
4.5 + 0.50y = 6
4.5 - 4.5 + 0.50y = 6 - 4.5
0.50y = 1.5
0.50y/0.50 = 1.5/0.50
y = 3
Again, x = 15 - y = 15 - 3 = 12
So far, you probably noticed that mixture word problems can be quite challenging!
Example #3:
You have 6 liters of water that have 20 percent strawberry juice. How many liters of a 80 percent strawberry juice should be added to the mixture to make 75 percent strawberry juice?
Solution: Use of two variables leading to a system of linear equations.
Le x be number of liters of water that contain 20 percent strawberry juice.
Let y represent number of liters of water that contain 80 percent strawberry juice.
x + y = 6
0.20x + 0.80y = 0.75 × 6
Solve by substitution
x = 6 - y
0.20 × (6 - y) + 0.80y = 4.5
0.20 × 6 - 0.20 × y + 0.80y = 4.5
1.2 + 0.80y - 0.20y = 4.5
1.2 + 0.60y = 4.5
1.2 - 1.2 + 0.60y = 4.5 - 1.2
0.60y = 3.3
0.60y / 0.60 = 3.3 / 0.60
y = 5.5
x = 6 - 5.5 = 0.5
Therefore, if you want your juice to contain 75% strawberry juice, do the following:
Mix 5.5 liters of water that has 80% strawberry juice with 0.5 liter of water that has 20% strawberry juice.
Your juice should taste better now!
The mixture word problems I solved above are typical questions. You may not encounter these word problems a lot in algebra. However, it is good idea to know how to solve these mixture word problems.
When solving mixture word problems, I suggest you do it with a system of linear equations.