Scale drawings
Before studying this lesson about scale drawings, you should review the lesson about solving proportions.
Since it is not always possible to draw on paper the actual size of real-life objects such as the real size of a car or an airplane, we need scale drawings to represent the size like the one you see below of a van.
In real-life, the length of this van may measure 240 inches. However, the length of a copy or print paper that you could use to draw this van is a little bit less than 12 inches.
Since 240/12 = 20, you will need about 20 sheets of copy paper to draw the length of the actual size of the van.
In order to use just one sheet, you could then use 1 inch on your drawing to represent 20 inches on the real-life object.
You can write this situation as 1:20 or 1/20 or 1 to 20.
When looking at 1:20, you can make the following observations:
Notice that the first number or the number on the left of the colon always refers to the length of the drawing on paper.
The second number or the number on the right of the colon refers to the length of the real-life object.
How to use scale drawings to solve real-life problems.
Example #1:
Suppose a problem tells you that the length of a vehicle is drawn to scale. The scale of the drawing is 1:20.
If the length of the drawing of the vehicle on paper is 12 inches, how long is the vehicle in real life?
Set up a proportion that will look like this:
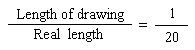
Do a cross product by multiplying the numerator of one fraction by the denominator of the other fraction
We get the following equation:
Length of drawing × 20 = Real length × 1
Since length of drawing = 12, we get:
12 × 20 = Real length × 1
240 inches = Real length
The real length of the vehicle is 240 inches.
Example #2:
The scale drawing of this tree is 1:500
If the height of the tree on paper is 20 inches, what is the height of the tree
in real life?
Set up a proportion like this:
Do a cross product by multiplying the numerator of one fraction by the denominator of the other fraction.
We get the following equation:
Height of drawing × 500 = Real height × 1
Since height of drawing = 20, we get:
20 × 500 = Real length × 1
10000 inches = Real height
The real length of the tree is 10000 inches.
The ratio 1/20 or 1/500 is called scale factor or scale ratio. It is a ratio of the size of the scaled drawing to the original size of the object.
You can quickly find the original size or the reduced size of an object using the scale factor.
Suppose the scale factor is 1/n.
To find the original size of an object, just multiply the reduced size by n.
To find the reduced size, just multiply the original size by 1/n.
Example #3:
A Honda odyssey is drawn on paper with a scale factor of 1/50. If the length of the vehicle on paper is 10.4 cm, what is the actual length of the Honda odyssey?
To find the actual length of the Honda odyssey, all you need to do is to multiply 10.4 cm by 50.
Since 10.4 times 50 is equal to 520 centimeters, the actual length of the Honda odyssey is 520 cm.
Example #4:
The actual distance between two cities is 5 km. What is the distance in centimeters between the two cities on the map if the scale ratio is 1/80000?
First convert 5 km to cm as shown below
km hm dam m dm cm
5 0 0 0 0 0
5 km = 500000 cm
To find the distance between the two cities on the map, all you need to do is to multiply 500000 by 1/80000.
500000 × 1/80000 = 500000/1 × 1/80000
500000 × 1/80000 = (500000 × 1) / (1 ×80000)
500000 × 1/80000 = 500000 / 80000
500000 × 1/80000 = 6.25
The distance between the two cities on the map is 6.25 cm.