Ratio and Proportion

Understanding Ratios and Proportions

A ratio is a comparison between two quantities, indicating how much of one thing there is compared to another. For example, if there are 2 apples and 3 oranges, the ratio of apples to oranges is 2:3. Proportion, on the other hand, states that two ratios are equal. It’s a way to show that two relationships are consistent or balanced. Proportions are particularly useful for solving problems involving scaling, comparing, and converting units.

Mastering ratios and proportions is crucial because these concepts form the backbone of various mathematical applications and everyday decision-making processes. Whether you're adjusting a recipe, budgeting finances, or engineering complex machinery, understanding how to manipulate and apply ratios and proportions can enhance your problem-solving skills and ensure accuracy in your calculations.

Real-Life Applications of Ratio and Proportion

Real-life applications of ratio and proportion are numerous! These mathematical concepts appear in various everyday activities and professional fields. Whether you're preparing recipes, painting your house, or repairing gears in a large machine or a car transmission, ratios and proportions play a crucial role.

Cooking and Recipes

Consider a recipe for brownies that requires 4 cups of flour to serve 6 people. If you want to serve 24 people, you need to determine how much flour to use. As a former math teacher, I used to advise my students to set it up as follows:

Setting Up a Proportion

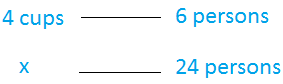
The setup can be translated into the following proportion:

4 cups x = 6 24

By solving this proportion, you can easily find the value of xxx, ensuring your recipe scales correctly without any errors. This method is fundamental in adjusting ingredient quantities to accommodate different serving sizes.

Painting and Home Improvement

Another practical application is painting. Suppose you need 4 gallons of paint to cover 1,000 square feet of your house. If you plan to paint 1,500 square feet, setting up a proportion helps determine the amount of paint required:

4 gallons x = 1000 1500

Solving this will give you the precise amount of paint needed, preventing waste and ensuring an even coat.

Mechanical Applications: Gears in Car Transmissions

Probably one of the most fascinating applications of ratio and proportion is found in the mechanics of car transmissions. Gears, which are circular with teeth around their edges, rely heavily on these concepts to function efficiently.

Gear theory in vehicle transmissions is a complex study, but here's a simplified overview. Transmissions contain several combinations of large and small gears. For example, if a small gear with 20 teeth drives a large gear with 40 teeth, the large gear will turn at half the speed of the small gear:

20 40 = 1 2

This ratio not only affects the speed but also increases the turning force, or torque, of the large gear. Generally, the larger the gear, the greater the torque it can produce. Understanding the ratio of gears helps determine both the speed and the torque each gear will deliver.

Practical Implications in Engineering

This concept is vital when assembling a transmission system. For instance, the gear ratio must be set correctly to move a load efficiently. At cruising speeds, gears may have the same ratio, ensuring that the torque entering the transmission equals the torque exiting it. Automotive engineers perform extensive gear ratio calculations to design effective and reliable transmissions.

Additional Applications

Beyond cooking, painting, and mechanical engineering, ratios and proportions are essential in fields like finance for calculating interest rates, in construction for scaling blueprints, and in healthcare for determining medication dosages. They provide a foundational tool for solving problems involving scaling, comparison, and distribution.