Simplifying algebraic expressions

Simplifying algebraic expressions with one or more variables by combining like terms is what this lesson will show you.  

How to simplify numerical expressions 

Let's say you want to simplify 5 + 5 + 5 + 5. What is a quick way to get the answer?

You can do 4 × 5 and 4 × 5 is a simplified version of 5 + 5 + 5 + 5.

If you had the following problem to simplify 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5, you can quickly see why it would be useful to just count how many fives there are and then times the amount by 5.

Since there are 11 fives, the simplified expression is 11 × 5

Relationship between simplifying numerical expressions and simplifying algebraic expressions

In the same manner, to simplify example #1, just count how many v's there are and multiply the amount by v.

Example #1:

Try to simplify v + v + v + v + v + v

Since there are 6 of them, v + v + v + v + v + v = 6 × v.

To simplify 6 × v even further, you can write 6v. However, remember that there is a multiplication between 6 and v.

What are like terms?

Example #2:

Now, try to simplify v + v + v + v + x + x + x

I hope it makes sense to you that you cannot add v and x. What is v + x?

You cannot say 2v because it is v + v that is equal to 2v.

You cannot say 2x because it is x + x that is equal to 2x

By the same token, there is another thing you need to watch for. What is v + 2? It is not 2v as already shown.

Again, v and 2 are not like terms either, so v + 2 = v + 2

However, since you can add all the v's, we call the v's like terms. It is the same for the x's. They are called like terms. You can use parenthesis to put together the like terms.

v + v + v + v + x + x + x = (v + v + v + v) + (x + x + x) = 4 × v + 3 × x = 4v + 3x

Example #3:

What about 4v + 3x + 5v + 4x?

You cannot add 4v to 3x, but you can add 4v to 5v. And you can add 3x to 4x

4v + 3x + 5v + 4x = 4v + 5v + 3x + 4x = 9v + 7x

For example what is xy + xy + xy + xy + xy + xy?

How many xy's do you see? Since there are 6 of them, xy + xy + xy + xy + xy + xy = 6xy

We do have a multiplication between x and y, but it does not change anything.

In the same way, 8xyzf + 12xyzf + xyzf + xyzf + xyzf = 20xyzf + 3xyzf = 23xyzf

Other important things to keep in mind when simplifying algebraic expressions

v + v + v + v + v + v = 1v + 1v + 1v + 1v + 1v + 1v = (1 + 1 + 1 + 1 + 1 + 1)v = 6v

This shows you a couple of things.

First, notice that putting a 1 next to each v will not change the answer.

1v = v.

Then, when simplifying algebraic expressions, you can just do your math with the number on the left on the variable.

Finally, when simplifying algebraic expressions, subtraction and/or putting negative numbers work pretty much the same way. You can only subtract like terms! The only difficulty you will encounter is the subtraction or addition of integers.

Example #4:

Simplify 4v - 3x - 2v + 4x

I can do 4v with 2v. However, be very careful! The operation on the left of 2v is subtraction, so you have to do 4v - 2v = 2v

In the same way, I can do 3x with 4x, but the operation next to 3x is subtraction. You have to change the subtraction to + -

Then, you will do -3x + 4x = 1x. I hope you have mastered how to add integers

4v - 3x - 2v + 4x = 2v + 1x

Useful guidelines when simplifying algebraic expressions

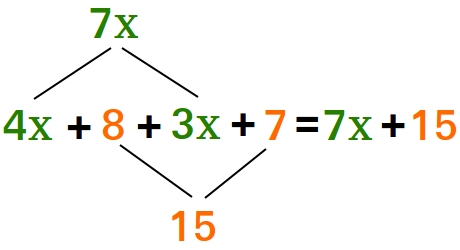
Step 1: Look for like terms

Step 2: Watch out for minus or negative sign next to variables (on the left of the variables)

Step 3: When you move this term around, you got to move it with the minus or negative sign as well

Step 4: Add or subtract only the integers on the left of the like terms.

More challenging problems about simplifying algebraic expressions

Example #5:

9x + 4 + 15v - 7x + 8 - 10v

First, put like terms together and then simplify

9x + 4 + 15v - 7x + 8 - 10v = 9x - 7x + 15v - 10v + 4 + 8 = 2x + 5v + 12

Example #6:

-5 - 6x - 5x + 10y - 4x + 1 + 10x + y

Put like terms together

-5 - 6x - 5x + 10y - 4x + 1 + 10x + y = -6x - 5x - 4x + 10x + 10y + y - 5 + 1

Just add all the numbers next to x, called coefficients.

-6 - 5 - 4 + 10 = -11 - 4 + 10 = -15 + 10 = -5

Then, add all the numbers next to y.

10 + 1 = 11

-5 - 6x - 5x + 10y - 4x + 1 + 10x + y = -5x + 11y + -4

Simplifying algebraic expressions with exponents

Example #7:

6x³ + 4y² + -2xy + 4y + -4x³ + y² + 6xy - 9y + x + 6

First, put the like terms together

6x³ + -4x³ + 4y² + y² + -2xy + 6xy + 4y - 9y + x + 6

Add the coefficients of the like terms

(6 + -4)x³ + (4 + 1)y² + (-2 + 6)xy + (4 - 9)y + x + 6

2x³ + 5y² + 4xy + -5y + x + 6

Simplifying algebraic expressions using the distributive property

Example #8:

5(x + 2y + -2) + 4(2x - y + 1)

First, use the distributive property to get rid of the parentheses.

5x + 10y + -10 + 8x - 4y + 4

Combine like terms

5x + 8x + 10y - 4y + -10 + 4

13x + 8y + -6

Simplifying algebraic expressions using the order of operations

Example #9:

2 × [(3x ÷ x × 2) - 4 × y] + -5 × 2 + 1

First, simplify -5 × 2 + 1 using the order of operations

2 × [(3x ÷ x × 2) - 4 × y] + -10 + 1

2 × [(3x ÷ x × 2) - 4 × y] + -9

Use the order of operations to simplify the expression inside the brackets

2 × [(3 × 2) - 4 × y] + -9

2 × [6 - 4 × y] + -9

2 × (6 - 4y) + -9

12 - 8y + -9

3 - 8y