Adding polynomials using algebra tiles, horizontally, and vertically

Adding polynomials by combining like terms together and using algebra tiles is the goal of this lesson. We will show you the following three ways to add polynomials.

  • Using algebra tiles
  • Adding vertically
  • Adding horizontally

Adding polynomials with algebra tiles

We will start with algebra tiles since the process is a lot more straightforward and concrete with tiles. To this end, study the model below with great care.

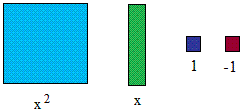
algebra tiles
Algebra tiles

Example #1:

Add 2x2 + 3x + 4 and 3x2 + x + 1

Step 1

Model both polynomials with tiles.

Adding polynomials with algebra tiles

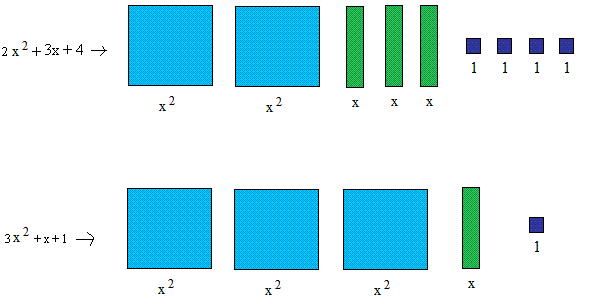
Step 2

Combine all tiles that are alike and count them.

  • You got a total of 5 light blue square tiles, so 5x2
  • You got a total of 4 green rectangle tiles, so 4x
  • You got a total of 5 blue small square tiles, so 5

Putting it all together, we get 5x2 + 4x + 5

I hope from the above modeling, it is clear that we can only combine tiles of the same type. For example, you could not add light blue square tiles to green rectangle tiles just like it would not make sense to add 5 potatoes to 5 apples. Try adding 5 potatoes to 5 apples and tell me if you got 10 apples or 10 potatoes. It just does not make sense!

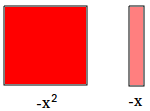
Example #2:

Add 2x2 + -3x + -4 and -3x2 + -x + 1

Step 1

Model both polynomials with tiles

Algebra tiles

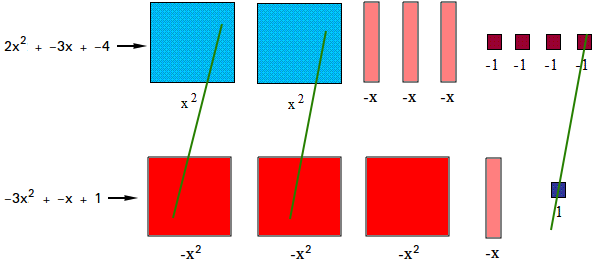
Step 2

Combine all tiles that are alike and count them. Tiles that are alike, but have different colors will cancel each other out. We show each cancellation with a green line.

  • You are left with of 1 red square tile, so -x2
  • You got a total of 4 light red rectangle tiles, so -4x
  • You are left with 3 strong pink small square tiles, so -3

Putting it all together, we get -x2 + -4x + -3

Keep these important facts in mind when adding polynomials

  • We call tiles that are alike or are the same type "like terms"
  • Like terms are terms with the same variable and the same exponent. For example, 2x2 and 3x2 in example #1 are like terms because they have the same variable, x and the same exponent, 2.
  • To add like term, just add the coefficients, or the numbers attached to the term, or the number on the left side of the term. 2x2 + 3x2 = (2 + 3)x2 = 5x2

Adding polynomials vertically


Example #3:

Add 6x2 + 8x + 9 and 2x2 + -13x + 2

Line up like terms. Then add the coefficients.

   6x2  +  8x    + 9
+ 2x2  + -13x  + 2
------------------------------
   8x2  + -5x    + 11


Example #4:

Add -5x3 + 4x2 + 6x + -8 and 3x3 + -2x2 + 4x + 12

Line up like terms. Then add the coefficients.

   -5x3 +  4x2 + 6x  + -8
+  3x3 + -2x2 + 4x  + 12
--------------------------------------
  -2x3  + 2x2 + 10x +  4

Adding polynomials horizontally


Example #5:

Add 6x2 + 2x + 4 and 10x2 + 5x + 6

Combine or group all like terms. You could use parentheses to keep things organized.

(6x2 + 2x + 4) + (10x2 + 5x + 6)  = (6x2 + 10x2) + (2x + 5x) + (4 + 6)

(6x2 + 2x + 4) + (10x2 + 5x + 6)  = (6 + 10)x2 + (2 + 5)x + (4 + 6)

Add the coefficient

(6x2 + 2x + 4) + (10x2 + 5x + 6)  = 16x2 + 7x + 10


Example #6:

Add 2x4 + 5x3 + -x2 + 9x + -6 and 10x4 + -5x3 + 3x2 + 6x + 7

(2x4 + 5x3 + -x2 + 9x + -6) + (10x4 + -5x3 + 3x2 + 6x + 7)

= (2x4 + 10x4) + (5x3 + -5x3) + (-x2 + 3x2) + (9x + 6x) + (-6 + 7)

= (2 + 10)x4 + (5 + -5)x3 + (-1 + 3)x2 + (9 + 6)x + (-6 + 7)

= (12)x4 + (0)x3 + (2)x2 + (15)x + (1)

= 12x4 + 2x2 + 15x + 1

Notice that if the term is x2, you can rewrite it as 1x2, so your coefficient is 1. We did this in example #6, third line with (-x2 + 3x2)

(-x2 + 3x2) = (-1x2 + 3x2)

Adding polynomials quiz

Subtracting polynomials