Subset of a Set
This lesson will explain what a subset of a set is. We will start our lesson with a definition.We write B ⊆ A
By definition, the empty set( { } or ∅ ) is a subset of every set.
Now, take a look at the following Venn diagrams.
Definition of Venn Diagrams:
Venn Diagrams are closed circles, named after English logician Robert Venn, used to represent relationships between sets.
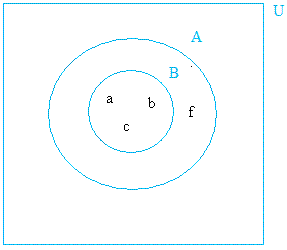
B = { a, b, c}
A = { a, b, c, f}
U = { a, b, c, f}
Since all elements of B belong to A, B is a subset of A.
Proper subset:
Set B is a proper subset of set A, if there exists an element in A that does not belong to B. We write B ⊂ A.
Having said that, B is a proper subset of A because f is in A, but not in B.
We write B ⊂ A instead of B ⊆ A.
Universal set:
The set that contains all elements being discussed.
In our example, U, made with a big rectangle, is the universal set.
Set A is also a proper subset of U because not all elements of U are in subset A.
Notice that B can still be a subset of A even if the circle used to represent set B was not inside the circle used to represent A. This is illustrated below:
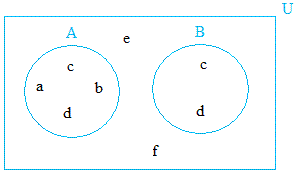
As you can see, B is still a subset of A because all its objects or elements (c, and d) are also objects or elements of A.
B is again a proper subset of A because there are elements of A that does not belong to B.
A and B are also subsets of the universal set U, but especially proper subsets since there are elements in U that does not belong to A and B.
In general, it is better to represent the figure above as shown below to avoid being redundant.
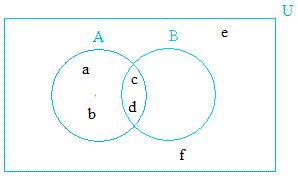
The area where elements c, and d are located is the intersection of A and B. More on this on a different lesson!
If you have any questions about this lesson, I will be more than happy to answer them.