Surface area of a cylinder
The surface area of a cylinder is the total area of the surface of the cylinder. The surface of a cylinder consists of two congruent parallel bases and the curved surface of the cylinder. The parallel bases are circles and the curved surface is also called lateral surface of a cylinder.
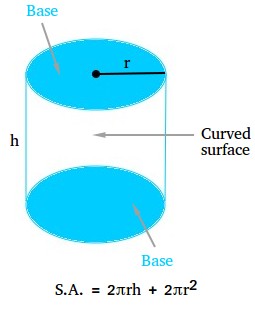
Surface area of a cylinder formula
The total surface area of a cylinder is the sum of the lateral area (curved surface) and the areas of the two circular bases.
The lateral area of a cylinder is the product of the circumference of the base and the height of the cylinder.
Lateral area = L.A. = 2πrh or L.A. = πdh since d = 2r.
Let B be the area of one base. The areas of the bases = 2B = πr2 + πr2 = 2πr2
Total surface area of a cylinder (TSA) = S.A. = L.A. + 2B = 2πrh + 2πr2
The surface area is expressed in square units.
- If r and h are measured in meters, then the surface area is measured in square meters or m2.
- If r and h are measured in centimeters, then the surface area is measured in square centimeters or cm2.
- If r and h are measured in inches, then the surface area are measured in square inches or in.2
Derivation of the surface area of a cylinder
To derive the formula of the surface area of a cylinder, we will start by showing you how you can make a cylinder. Start with the net of a cylinder consisting of a rectangle and two congruent circles.
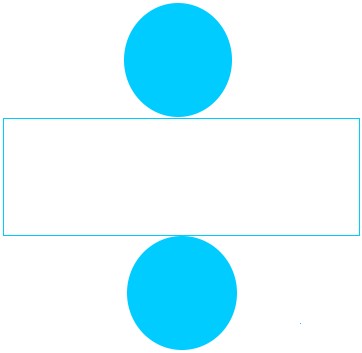
Then, fold the rectangle until you make an open cylinder with it. An open cylinder is a cylinder that has no bases. A good real life example of an open cylinder is a pipe that is used to flow water if you have seen one before.
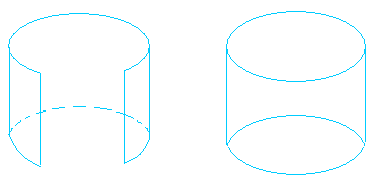
Next, using the two circles as bases for the cylinder, put one on top of the cylinder and put one beneath it.
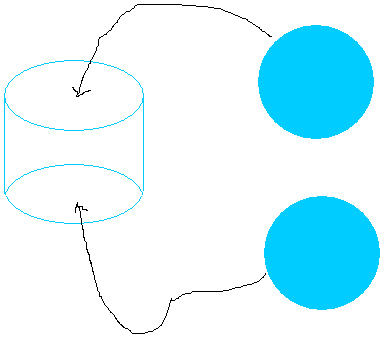
Of course, the two circles will have the exact same size or the same diameter as the circles obtained by folding the rectangle.

Now, what did we go through so much trouble? Well if you can make the cylinder with the rectangle and the two circles, you can use them to derive the surface area of the cylinder. Does that make sense?
The area of the two circles is straightforward. The area of one circle is pi × r2, so for two circles, you get 2 × pi × r2
To find the area of the rectangle is a little bit tricky and subtle!
Let us take a closer look at our rectangle again.
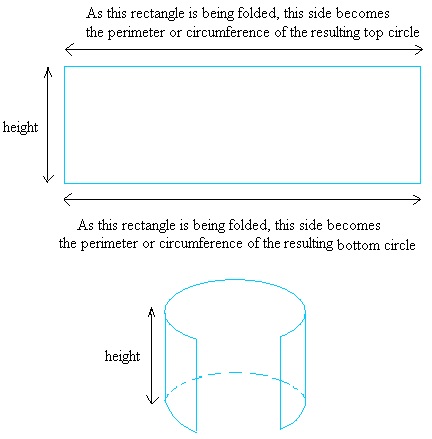
To get the area of the rectangle, multiply h by 2 × pi × r and that is equal to 2 × pi × r × h
Therefore, the total surface area of the cylinder, call it S.A. is:
S.A. = 2 × pi × r2 + 2 × pi × r × h
A couple of examples showing how to find the surface area of a cylinder.
Example #1:
Find the surface area of a cylinder with a radius of 2 cm, and a height of 1 cm
SA = 2 × pi × r2 + 2 × pi × r × h
SA = 2 × 3.14 × 22 + 2 × 3.14 × 2 × 1
SA = 6.28 × 4 + 6.28 × 2
SA = 25.12 + 12.56
Surface area = 37.68 cm2
Example #2:
Find the surface area of a cylinder with a radius of 4 cm, and a height of 3 cm
SA = 2 × pi × r2 + 2 × pi × r × h
SA = 2 × 3.14 × 42 + 2 × 3.14 × 4 × 3
SA = 6.28 × 16 + 6.28 × 12
SA = 100.48 + 75.36
Surface area = 175.84 cm2
Surface area of an oblique cylinder
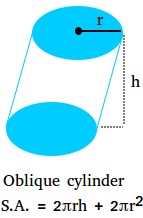
An oblique cylinder is a cylinder whose side is not perpendicular to its base. The surface area of an oblique cylinder is still the same as the area of a right cylinder. Just make sure that the height of the cylinder is measured vertically.
S.A. = 2πrh + 2πr2
How to find the surface area of a hollow cylinder
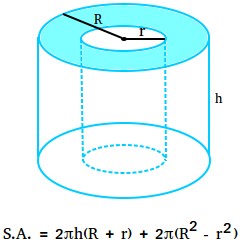
The area of one base is equal to the area of outer circle - the area of inner circle.
Area of one base = πR2 - πr2 = π(R2 - r2)
Area of two bases = π(R2 - r2) + π(R2 - r2) = 2π(R2 - r2)
Now, we need to find the lateral area of the hollow cylinder.
Since we are dealing with two cylinders instead of one, we need to find the lateral area of two cylinders.
L.A. of the outer cylinder is 2πRh and L.A. of the inner cylinder is 2πrh.
L.A. = 2πRh + 2πrh
Total surface area of the hollow cylinder is equal to L.A. + area of two bases
Total surface area of the hollow cylinder = 2πRh + 2πrh + 2π(R2 - r2)
Total surface area of the hollow cylinder = 2πh(R + r) + 2π(R2 - r2)