Undefined Slope
Undefined slope is so often misunderstood and many students find it confusing that I thought it would be a good thing to dedicate a special lesson to explain it.
As the lesson about "what is slope" shows, the 4 different types of slopes are positive slope, negative slope, zero slope and undefined slope.
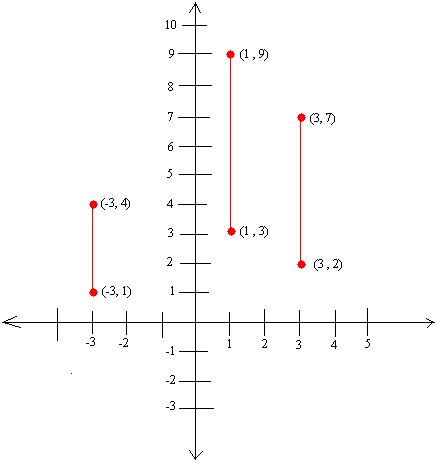
Basically, a slope that is undefined looks like the vertical lines on the coordinate system you see in the graph below.
When a slope is undefined all you do is moving straight up or straight down only. You are not moving horizontally at all. In other words, the run or horizontal change is zero. The slope is therefore at its steepest.
Real-Life Examples of Undefined Slope
- A good real life example of undefined slope is an elevator since an elevator can only move straight up or straight down.
- The walls in your bedroom or living room could also have a slope that is undefined since this is how these walls are usually built. A spirit level is used during construction to ensure the walls are as "vertical" as possible.
It got its name "undefined" from the fact that it is impossible to divide by zero. This can happen when the denominator is zero.
Recall that 6/2 equal 3 because 3 × 2 = 6
However, it is impossible to do 8/0 because there exists no number you can multiply 0 by to get 8. We say that this division is undefined.
Using the Slope Formula to Show that each of the Vertical Lines above has an Undefined Slope
Now, let us try to get the slope for the lines above. Recall that the slope formula is
m = (y1 − y2)/(x1 − x2)
For the line on the left, the points are (-3, 4) and (-3, 1)
Let x1 = -3 , y1 = 4 and x2 = -3 and y2 = 1
m = (y1 − y2)/(x1 − x2)
m = (4 − 1)/(-3 − -3)
m = (4 − 1)/(-3 + 3)
m = 3/0
The denominator is zero. As a result, there exists no number you can multiply 0 by to get 3. Therefore, we say that the slope is undefined.
For the line in the middle, the points are (1, 3) and (1, 9)
Let x1 = 1 , y1 = 9 and x2 = 1 and y2 = 3
m = (y1 − y2)/(x1 − x2)
m = (9 − 3)/(1 − 1)
m = 6/0
The denominator is zero. As a result, there exists no number you can multiply 0 by to get 6. Therefore, we say that the slope is undefined.
For the line on the right, the points are (3, 7) and (3, 2)
Let x1 = 3 , y1 = 7 and x2 = 3 and y2 = 2
m = (y1 − y2)/(x1 − x2)
m = (7 − 2)/(3 − 3)
m = 5/0
The denominator is zero. As a result, there exists no number you can multiply 0 by to get 5. Therefore, we say that the slope is undefined.
Notice that for the line in the middle, the x-values are the same for both points.
x1 = x2 = 1
This is also the case for all the lines above.
In general, when the x-values or x-coordinates are the same for all points on a line, the slope is undefined. If you can make this observation, there is no need to compute the slope.
Undefined Slope Equation
Is it possible to write a line with an undefined slope in slope-intercept form or point-slope form?
Since the slope m cannot be found, this is not possible. However, you can still write an equation for the line.
The equation of a line with an undefined slope is x = x-coordinate. Notice that the y-coordinates can equal to any real number.
Example
Write an equation of the line with undefined slope and passing through (-2, 4), (-2,0), and (-2, -4)
Since the x-coordinate is -2, the equation of the line is x = -2