Vertical angles theorem
The vertical angles theorem is about angles that are opposite each other. We explain the concept, provide a proof, and show how to use it to solve problems.
These vertical angles are formed when two lines cross each other as you can see in the following drawing.
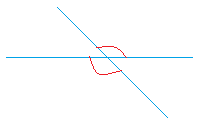
Theorem: Vertical angles are congruent.
Congruent is quite a fancy word. Put simply, it means that vertical angles are equal. For example, look at the two angles in red above. They have the same measure.
If one of them measures 140 degrees such as the one on top, the one at the bottom is also 140 degrees.
Vertical angles theorem proof
The proof is simple. The proof will start with what you already know about straight lines and angles.
We will use the angle addition postulate and the substitution property of equality to arrive at the conclusion.
The angle addition postulate states that if two adjacent angles form a straight angle, then the two angles will add up to 180 degrees .
The substitution property states that if x = y, then y can replace x in any expression. Or x can replace y in any expression.
Use this figure for the proof.
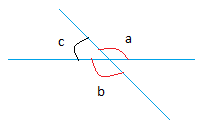
Given: ∠ a and ∠ b are vertical angles
Prove m ∠ a = m ∠b
Note that m ∠ a means measure of angle a
By the angle addition postulate,
m ∠ a + m ∠ c = 180 degrees
m ∠ b + m ∠ c = 180 degrees
By substitution, m ∠ a + m ∠ c can replace 180 degrees in the equation at the bottom.
We get:
m ∠ b + m ∠ c = m ∠ a + m ∠ c
Subtract m ∠ c from both sides of the equation
m ∠ b + m ∠ c - m ∠ c = m ∠ a + m ∠ c - m ∠ c
m ∠ b = m ∠ a
Using the vertical angles theorem to solve a problem
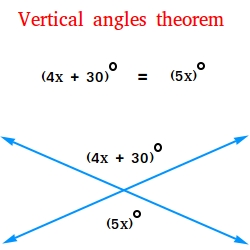
Use the vertical angles theorem to find the measures of the two vertical angles.
Since vertical angles are congruent or equal, 5x = 4x + 30
5x = 4x + 30
Subtract 4x from each side of the equation
5x - 4x = 4x - 4x + 30
x = 30
Use 4x + 30 to find the measures of the vertical angles
4 times 30 + 30 = 120 + 30 = 150
The two vertical angles measure 150 degrees.