Exponents
Exponents can make your math problems a lot easier to handle. Simply put, it is a shortcut for multiplying numbers over and over again.
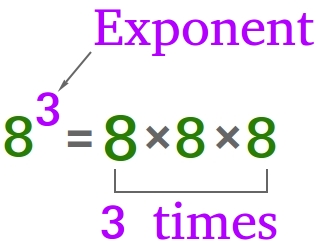
8 × 8 × 8 × 8 × 8 × 8
Instead of multiplying 8 six times by itself, we can just write 86 and it will mean the same thing.
When reading 86, we say eight to the sixth power or eight to the power of six.
In a similar way, 12 × 12 × 12 × 12 × 12 × 12 × 12 × 12 × 12 × 12 = 1210
In 1210, 12 is called the base and 10 is called the exponent.
Other examples of exponents:
53 = 5 × 5 × 5
94 = 9 × 9 × 9 × 9
72 = 7 × 7
66 = 6 × 6 × 6 × 6 × 6 × 6 × 6
28 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
In general,
yn = y × y × y × y ×...× y × y (n times)
In one of the examples above, it says 72 = 7 × 7yn = y × y × y × y ×...× y × y (n times)
What would you say 71 is equal to?
For 72, you wrote down 7 twice.
Therefore, for 71, you will write down 7 once and of course there is no need to have a multiplication sign.
71 = 7
Common pitfalls to avoid when working with exponents:
What is -26 equals to?
Is it equal to -2 × -2 × -2 × -2 × -2 × -2 ?
Or is it equal to -(2 × 2 × 2 × 2 × 2 × 2) ?
It is equal to -(2 × 2 × 2 × 2 × 2 × 2) = -(26) = - 64
However, (-2)6 is a different story.
(-2)6 = (-2) × (-2) × (-2) × (-2) × (-2) × (-2) = - × - × - × - × - × - × 2 × 2 × 2 × 2 × 2 × 2
Notice that - × - = +
So, - × - × - × - × - × - × 2 × 2 × 2 × 2 × 2 × 2 = + × + × + × 26
Note that + × + = +
(-2)6 = +26
In (-2)6, the exponent is even. Change it to any odd number and the answer will be negative.
(-2)7 = (-2) × (-2) × (-2) × (-2) × (-2) × (-2)× (-2) = - × - × - × - × - × - × - × 2 × 2 × 2 × 2 × 2 × 2 × 2
- × - × - × - × - × - × - × 2 × 2 × 2 × 2 × 2 × 2 × 2 = + × + × + × - × 27
+ × + × + × - × 27 = + × - × 27
Note that + × - = -
+ × - × 27 = -27
Important observations about exponents:
- -an is always negative.
- (-a)n is either negative or positive. It is positive if n is an even number. It is negative if n is an odd number.
- -an is not always equal to (-a)n
- -an may equal to (-a)n only when n is an odd number.
When the base is a fraction it is common to use parentheses as shown below:
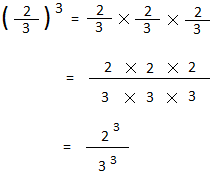 |
The above is also equal to
8
27

