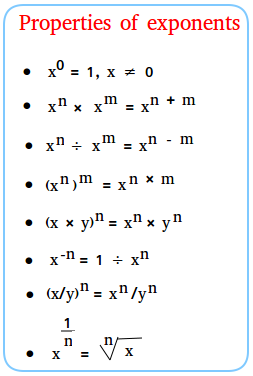Properties of exponents

We will show 8 properties of exponents. Let x and y be numbers that are not equal to zero and let n and m be any integers. We also assume that no denominators are equal to zero. First, we go over each property and give examples to show how to use each property. Then, at the end of this lesson, we summarize the properties.

Property #1

x⁰ = 1

Examples:

4⁰ = 1

(2500000000000000000000)⁰ = 1

(x² + 5x + 6)⁰ = 1

Property #2

xⁿ × x^m = x^{n + m}

Examples:

4⁶ × 4⁵ = 4^{6 + 5} = 4¹¹

3² × 3^-8 = 3^2+-8 = 3^-6

(x + y)¹⁰ × (x + y)^-5 = (x + y)^10+-5 = (x + y)⁵

Property #3

xⁿ ÷ x^m = x^{n − m}

Examples:

4⁶ ÷ 4⁵ = 4^{6 − 5} = 4¹

9⁴ ÷ 9^-3 = 9^4-(-3) = 9⁴⁺⁽⁺³⁾ = 9⁷

(a - b)⁸ ÷ (a - b)⁷ = (a - b)^8-7= (a - b)¹ = (a - b)

Property #4

(xⁿ)^m = x^{n × m}

Examples:

(5²)⁴ = 5^{2 × 4} = 5⁸

(6²)⁴ = 6^2×4 = 6⁸

(2x^-5)^-6 = (2x)^-5×-6 = (2x)³⁰

Property #5

(x × y)ⁿ = xⁿ × yⁿ

Examples:

(6 × 7)⁵ = 6⁵ × 7⁵

(12 × 10)^-4 = 12^-4 × 10^-4

[(x+y) × (a+b)]⁶ = (x + y)⁶ × (a + b)⁶

Property #6

x^-n = 1 ÷(xⁿ) = 1/(xⁿ)

Examples:

8^-4 = 1 ÷ (8⁴) = 1 / (8⁴)

15^-4 = 1÷15⁴ = 1/15⁴

(ax² + bx + c)^-3 = 1÷(ax² + bx + c)³ = 1/(ax² + bx + c)³ 

Property #7

(x/y)ⁿ = xⁿ / yⁿ

Examples:

(8/5)⁴ = 8⁴ / 5⁴

(12/5)^-4 = 12^-4/5^-4

[(x+a)/(y+b)]³ = (x+a)³/(y+b)³

Property #8

Here is a table that Summarize the properties of exponents.

Any questions about properties of exponents? Let me know.