Proof of the area of a triangle
A good way to start off with the proof of the area of a triangle is to use the area of a rectangle to quickly derive the area of a right triangle.
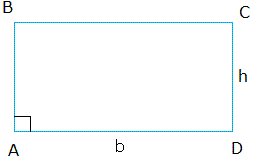
The area of this rectangle is b × h
However, if we draw a diagonal from one vertex, it will break the rectangle into two congruent or equal triangles.
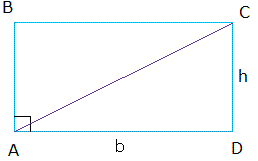
The area of each triangle is half the area of the rectangle. For example, the area of triangle ABC is 1/2(b × h). Does that make sense?
Although it does make sense, the proof is incomplete because triangle ABC is a right triangle or what we can also call a special triangle.
How do we know the formula is going to work for any triangle, such as isosceles, equilateral, or scalene triangles?
If we can prove that the formula is the same for any arbitrary triangle such as a scalene triangle which has nothing particular about it, then it will work for special triangles such as isosceles, equilateral, or right triangle.
Here is the best way to show a proof of the area of a triangle.
Let us start this time with a scalene triangle ABC which has nothing special about it.
Then, draw the height from vertex B and label it as you see below:
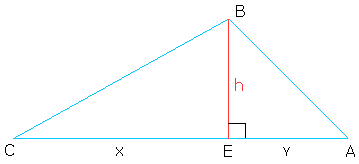
area of triangle ABC = area of triangle ABE + area of triangle CBE
area of triangle ABC = (y × h)/2 + (x × h)/2
area of triangle ABC = (y × h + x × h)/2
area of triangle ABC = h ×(y + x)/2
Notice that y + x is the length of the base of triangle ABC.
Thus, it is ok to say that y + x = b
Therefore, area of triangle ABC = (h × b)/2
Proof of the area of a triangle has come to completion yet we can go one step further.
How to prove that the area of a triangle can also be written as 1/2(b×a sin A)
At this point, most of the work is already done. All we need to do is to use a trigonometric ratio to rewrite the formula.
Consider again triangle ABC and find sin A.
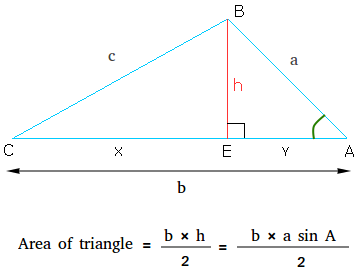
sin A = h / a and after multiplying both sides by a, we get h = a sin A.
Substitute a sin A for h in the formula and we are done!