Proof of the area of a parallelogram

Start your proof of the area of a parallelogram by drawing a parallelogram ABCD.
Then, draw heights from vertices D and C to segment AB. You may have to extend segment AB as you draw the height from C.


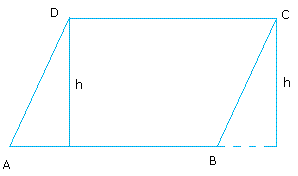
Call the rectangle that is formed by drawing the heights from vertices D and C, EDCF.


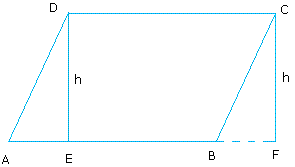
The proof is not complicated. We already know that the area of the rectangle is equal to base times height.

Therefore, if we can show that we can play with parallelogram ABCD to make rectangle EDCF, then we are done.

In this case, area of parallelogram ABCD must equal area of rectangle EDCF.

What we are trying to do is illustrated below:




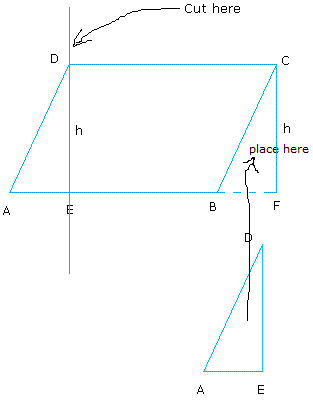
Carefully look at the figure again. Do you think that triangle ADE is the same as triangle FCB? It may be, but we need to prove it.

If triangle ADE is the same as triangle FCB, you could just cut triangle ADE and place it over triangle FCB until they coincide and here we go!

You had just made your rectangle by cutting triangle ADE from the parallelogram ABCD.

And again, if you can do that, both the parallelogram and the rectangle must have the same area.

All we have to do now is to show that triangle ADE is the same as triangle FCB and we are done!

We can use SSS postulate to show that triangle ADE and triangle FCB are congruent.

Both triangles are right triangles. If we can show that two sides are the same, the last side of the triangles will be the same after we use Pythagorean Theorem to find it. Both triangles will therefore be the same.

In parallelogram ABCD, segment AD = segment BC because in a parallelogram opposite sides are equal

In rectangle, EDCF, segment ED = segment FC because in a rectangle opposite sides are equal

We have found two sides that are equal! We are done with the whole proof.

Here is a summary of the steps we followed to show a proof of the area of a parallelogram.

1. Draw a parallelogram.
2. Cut a right triangle from the parallelogram. 
3. Use the right triangle to turn the parallelogram into a rectangle.
4. The parallelogram will have the same area as the rectangle you created that is b × h