Roman numeration system
The Roman numeration system evolved around 500 BCE. Just like other ancient numeration systems, it uses special symbols to represent numbers.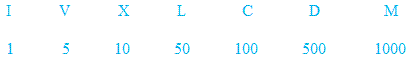
Any other roman numerals are found by combining these basic numerals.
More examples showing how the Roman numeration system works
1) 154 is equivalent to CLIIII in Roman numerals.2) 1492 is equivalent to MCCCCLXXXXII in Roman numerals.
3) 3495 is equivalent to MMMCCCCLXXXXV in Roman numerals.
Over time, two useful attributes were introduced that made the Roman numeration system very useful and efficient.
The first one is the subtractive principle
With the subtractive principle, Roman numerals can be combined or paired so that when reading from left to right, the values of the symbols in any pair increase.
The value of the new pair is bigger number in the pair − smaller number in the pair.
For instance, I can pair I and V to make IV and the value of this pair will be V − I = 5 − 1 = 4
I can pair C and D to make CD and the value of this pair will be D − C = 500 − 100 = 400
I can pair X and L to make XL and the value of this pair will L − X = 50 − 10 = 40
This subtractive principle will make the writing of examples 1), 2), and 3) a lot simpler.
1) CLIIII = CLIV
2) MCCCCLXXXII
Instead of CCCC, we can pair C and D to get CD and CD = 400 as demonstrated above.
Also, instead of LXXXX, we can pair X and C to make XC since XC still equal to 90.
Replacing CCCC (in bold) by CD, we get:
MCCCCLXXXII = MCDLXXXXII
Replacing LXXXX by XC (in blue), we get:
MCDLXXXXII= MCDXCII
So, instead of using 11 symbols, we can just use 7 to represent the same number.
3) MMMCCCCLXXXXV = MMMCDXCV
The second one is the multiplicative principle
Basically, a horizontal bar above any number means 1000 times the number.
Examples:
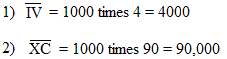
Notice how a bar on top of IV means that we need to multiply 4 by 1000.