Segment addition postulate
The segment addition postulate states the following for 3 points that are collinear.
|
|
 |
If 3 points A, B, and C are collinear and B is between A and C, then
AB + BC = AC
Using the segment addition postulate to solve a problem.
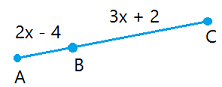
Suppose AC = 48, find the value of x. Then, find the length of AB and the length of BC.
AB + BC = AC
( 2x - 4 ) + ( 3x + 2 ) = 48
2x + 3x - 4 + 2 = 48
5x - 4 + 2 = 48
Add 4 to both sides of the equation.
5x - 4 + 4 + 2 = 48 + 4
5x + 2 = 52
Subtract 2 from both sides.
5x + 2 - 2 = 52 - 2
5x = 50
Divide both sides by 5
5x / 5 = 50 / 5
x = 10
Now that we have the value of x, we can find the length of AB and the length of BC.
AB = 2x - 4
AB = 2 × 10 - 4
AB = 20 - 4 = 16
The length of AB is 16
BC = 3x + 2
BC = 3 × 10 + 2
BC = 30 + 2 = 32
The length of BC is 32.
Segment addition postulate and the midpoint
Suppose XA = 3x and AY = 4x - 6. If A is the midpoint of XY, what is the length of XY?
3x 4x - 6
_________________________________
X A Y
The trick in this problem is to see that if A is the midpoint, then XA = AY.
Since XA = AY, 3x = 4x - 6
Subtract 3x from both sides.
3x - 3x = 4x - 3x - 6
0 = x - 6
Add 6 to both sides of the equation.
0 + 6 = x - 6 + 6
6 = x
To compute XA, you can either use 3x or 4x - 6
Using 3x, we get XA = AY = 3 × 6 = 16
Using 4x - 6, we get XA = AY = 3 × 6 - 6 = 18 - 6 = 12
XY = XA + AY = 16 + 16 = 32
The length of XY is 32.

