Geometry postulates

Geometry postulates, or axioms, are accepted statements or facts. Thus, there is no need to prove them. For example, the following statements are axioms:

  • Human beings cannot live without oxygen.
  • The sun sets in the west.
  • Human beings are more intelligent than reptiles.

Here are ten important geometry postulates that you absolutely need to know

Postulate 1.1

Through two points, there is exactly 1 line. Line t is the only line passing through E and F.

Postulate 1.1Postulate 1.1


Postulate 1.2

Two lines can meet or intersect in exactly 1 point. In the figure below, the point of intersection is called A.

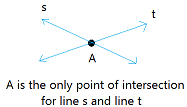Postulate 1.2Postulate 1.2


Postulate 1.3

Two planes can intersect in exactly 1 line. The figure below has 2 planes. Plane ZXY in yellow and plane PXY in blue intersect in line XY shown in red.

Postulate 1.3

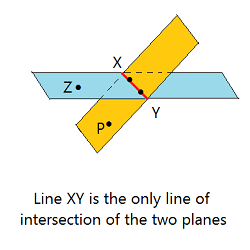
Postulate 1.4

Through any three points that are not on the same line, there is exactly one plane. Notice that we don't need 4 points to define a plane. This makes sense since a chair with only 3 legs will not fall over.

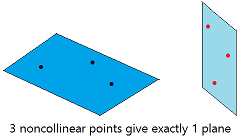Postulate 1.4Postulate 1.4

The 3 black points determine exactly 1 plane. The 3 red points determine exactly 1 plane.


Postulate 1.5 or ruler postulate

Each point on a line can be assigned a real number. The distance between any 2 points is the absolute value of the difference of the corresponding numbers.

Ruler postulate


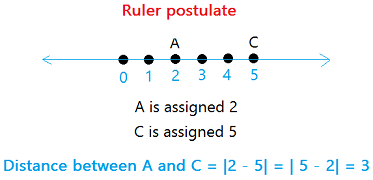
Postulate 1.6 or segment addition postulate

If A, B, and C are collinear, and B is between A and C, AB + BC = AC

For a more thorough coverage of the ruler postulate, check the link above.

Postulate 1.7 or protractor postulate

Let O be the midpoint of line AB.  Rays OA, OB, and all the rays with endpoints O that can be drawn on one side of line AB can be paired with the real numbers from 0 to 180 such that OA is paired with 0 degree and OB is paired with 180 degrees. 


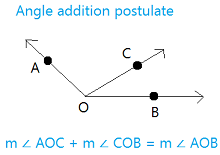
Postulate 1.8 or angle addition postulate

∠ AOC + m ∠ COB = m ∠ AOB

If ∠ AOB is a straight angle, then m ∠ AOC + m ∠ COB = 180


Postulate 1.9

If two shapes are congruent, then their areas are equal. For instance, a rectangle with width = 2 and height = 5 is congruent to a rectangle with width = 5 and height = 2.


Postulate 1.10

The area of a shape is the sum of the areas of its nonoverlapping parts.

Geometry proofs