Fibonacci sequence
The Fibonacci sequence is a famous mathematical sequence in which the first two terms are 1 and 1 and then each term after that is found by adding the previous two terms. The first 10 terms are shown in the figure below:
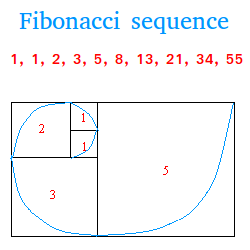
It is a naturally occurring phenomena in nature that was discovered by Leonardo Fibonacci. Leonardo was an Italian mathematician who lived from about 1180 to about 1250 CE.
Mathematicians today are still finding interesting way this series of numbers can describe nature. To see how this sequence describes nature, take a close look at the figure above.
This spiral shape is found in many flowers, pine cones, and snails' shell to mention just a few.
What exactly is happening here as far as math is concerned? You can see that we begin with two squares with a side length that is equal to 1.
Then, to get the side length of the third square, we add the side lengths of the two previous squares that is 1 and 1 (1 + 1 = 2)
To get the side length of a fourth square, we add 1 and 2 (1 + 2 = 3)
To get the side length of a fifth square, we add 2 and 3 (2 + 3 = 5)
If we continue this pattern we get:
- 3 + 5 = 8
- 5 + 8 = 13
- 8 + 13 = 21
- 13 + 21 = 34
- 21 + 34 = 55
- 34 + 55 = 89
- 55 + 89 = 144
- 89 + 144 = 233
Here is a short list of the Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233
As already stated, each number in the sequence is the sum of the two numbers before it.
We can try to derive a Fibonacci sequence formula by making some observations.
F1 = 1F2 = 1
F3 = F2 + F1 = 1 + 1 = 2
F4 = F3 + F2 = 2 + 1 = 3
F5 = F4 + F3 = 3 + 2 = 5
F6 = F6-1 + F6-2 = F5 + F4 = 5 + 3 = 8
F7 = F7-1 + F7-2 = 8 + 5 = 13
......
......
......
Fn = Fn-1 + Fn-2
The recursive formula for the Fibonacci sequence is Fn = Fn-1 + Fn-2 with F1 = 1 and F2 = 1
How to find the sum of the first ten terms of the Fibonacci sequence
1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 + 34 + 55 = 143Now, we will choose numbers other than 1 and 1 to create other Fibonacci-like sequences
2, 2, 4, 6, 10, 16, 26, 42, 68, 110
The sum is 2 + 2 + 4 + 6 + 10 + 16 + 26 + 42 + 68 + 110 = 286
what if we start with 3 and 3?
3, 3, 6, 9, 15, 24, 39, 63, 102, 165
3 + 3 + 6 + 9 + 15 + 24 + 39 + 63 + 102 + 165 = 429
Now, we shall make a nice observation?
143/11 = 13
286/11 = 26
429/11 = 39
143 = 11 × 13 = 11 × 13 × 1
286 = 11 × 26 = 11 × 13 × 2
429 = 11 × 39 = 11 × 13 × 3
You can thus see that the sum of the first 10 terms follow this pattern
11× 13 × 1
11× 13 × 2
11× 13 × 3
11× 13 × 4
......
......
......
11× 13 × 4
11 × 13 × n
Just remember that n = 1 is the Fibonacci sequence starting with 1 and 1
n = 2 is the one starting with 2 and 2
And so forth....

